QUESTÕES VESTIBULAR Ueg 2016 – COMENTADAS

 

1. (Ueg 2016)  Dados os conjuntos A = {x ε R/ -2 < x ≤ 4} e B = {x ε R/x > 0}  a intersecção entre eles é dada pelo conjunto :

a) {x ε R / 0 < x ≤ 4}   

b) {x ε R / x > 0}     

c) {x ε R / x > -2}     

d) {x ε R / x ≥ 4}    

Resposta da questão 1:[A]

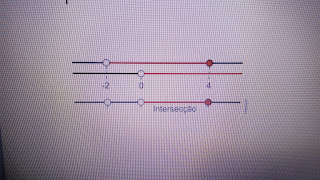
A intersecção dos dois conjuntos é {x ε R/0 < x ≤ 4}. Ou graficamente:

 

2. (Ueg 2016)  Em uma pesquisa realizada com 35 moradores na periferia de uma grande cidade para saberem a modalidade de leitura que realizam regularmente entre jornal, revista e outros livros, foi constatado que: 15 pessoas leem jornal, 17 pessoas leem revista, 14 pessoas leem outros livros, 7 pessoas leem jornal e revista, 6 pessoas leem revista e outros livros, e 5 pessoas leem jornal, revistas e outros livros. Diante dessas informações verifica-se que :

a) 5 pessoas não leem nenhuma das três modalidades.   

b) 4 pessoas não leem nenhuma das três modalidades.   

c) 3 pessoas não leem nenhuma das três modalidades.   

d) 2 pessoas não leem nenhuma das três modalidades.   

e) 1 pessoa não lê nenhuma das três modalidades.   

Resposta da questão 2: [D]

Admitindo que o número de pessoas que leem jornal e outros livros seja zero, temos o seguinte diagrama.

 

Sendo x o número de pessoas que não leem nenhuma das publicações, temos: 5 + 1 + 2 + 0 + 8 + 9 +8 + x = 35 → x = 2.

 

3. (Ueg 2016)  No primeiro semestre de 2015, a empresa “Aço Firme” fabricou 28000  chapas metálicas em janeiro; em fevereiro sua produção começou a cair como uma progressão aritmética decrescente, de forma que em julho a sua produção foi de 8800 chapas. Nessas condições, a produção da empresa nos meses de maio e junho totalizou :

a) 33600 chapas   

b) 32400 chapas   

c) 27200 chapas   

d) 24400 chapas   

e) 22600 chapas   

  

Resposta da questão 3:[C]

Considerando que a_n representa o número de chapas metálicas fabricadas no mês n, e que n=1 indica o mês de janeiro, n=2  o mês de fevereiro e assim por diante, temos:

a₇ = a₁ + 6r → 8800 = 28000 + 6r → - 19200 = 6r → r = - 3200

Logo:

a₅ = a₁ + 4r = 28000 + 4.(-3200) = 15200

a₆ = a₁ + 5r = 28000 + 5.(-3200) = 12000

Portanto, a soma pedida será: a₅  + a₆  = 15200 + 12000 = 27200 chapas

4. (Ueg 2016)  Um processo de produção é modelado pela seguinte função f(t) = -αt² + 160αt, em que t é a temperatura do processo em graus Celsius e α é uma constante positiva. Para que se atinja o máximo da produção, a temperatura deve ser :

a) -40⁰C  

b) -80⁰C      

c)  0⁰C    

d)  40⁰C      

e)  80⁰C      

Resposta da questão 4:[E]

A função f(t) é representada por uma parábola de concavidade para baixo e o valor de t para o qual f(t) é máximo será dado pela abscissa do vértice dessa função, ou seja: t = - 160α / -2α = 80⁰C.

  

  

5. (Ueg 2016)  A função f(x)  que representa o gráfico a seguir, onde k  é uma constante não nula, é dada por:

 

 

a) f(x) = kx/2, se 0 ≤ x ≤ 2 e f(x) = k, se 2 < x ≤ 5   

b) f(x) = kx/2, se 0 ≤ x ≤ 2 e f(x) = k, se 2 < x ≤ 5      

c) f(x) = kx/2, se 0 ≤ x ≤ 2 e f(x) = k, se 2 < x ≤ 5      

d) f(x) = kx/2, se 0 ≤ x ≤ 2 e f(x) = k, se 2 < x ≤ 5      

e) f(x) = kx/2, se 0 ≤ x ≤ 2 e f(x) = 2k, se 2 < x ≤ 5      

  

Resposta da questão 5:[A]

Determinando a lei de formação da função para valores de x tal que:  

0 ≤ x ≤ 2.

A reta para este intervalo é da forma y = ax, onde a  será dado por a = (k-0)/(2-0) e y = kx/2.

A lei de formação função para 2 < x ≤ 5  será dada por y = k (constante).

Logo, a lei de formação da função será dada por:

f(x) = kx/2, se 0 ≤ x ≤ 2 e f(x) = k, se 2 < x ≤ 5  

6. (Ueg 2016)  Na figura a seguir, é apresentado o gráfico de uma função f, de R  em R .

 

A função f é dada por :

a) f(x) = |2x + 2|, se x < 0  e f(x) = |x-2|, se x ≥ 0   

b) f(x) = - |x| + 2, se -1 ≤ x < 2  e f(x) = |2x-3|, se x < -1 e x ≥ 2     

c) f(x) = |x-1|, se x < 0  e f(x) = |x+2|, se x ≥ 0      

d) f(x) = - |x + 2|, se -1 ≤ x < 2  e f(x) = |2x| + 1, se x < -1 e x ≥ 2

Resposta da questão 6:[A]

Observando o gráfico percebe-se que a função pode ser descrita como:

f(x) = | 2x + 2 |, se x < 0 e f(x) = | x - 2 |, se x ≥ 0

Substituindo os valores que cruzam os eixos, percebe-se que eles conferem com o gráfico:

Quando x = -1, | 2.(-1) + 2 | = 0

Quando x = 0 , | 0 – 2 | = 2

Quando x = 2, | 2 - 2 | = 0

7. (Ueg 2016)  Tatiana e Tiago comunicam-se entre si por meio de um código próprio dado pela resolução do produto entre as matrizes A e B, ambas de ordem 2x2 onde cada letra do alfabeto corresponde a um número, isto é, a=1, b=2, c=3, ..., z=26. Por exemplo, se a resolução de A.B for igual a ab₁₁ =1, ab₁₂=13, ab₂₁=15 e ab₂₂=18, logo a mensagem recebida é amor. Dessa forma, se a mensagem recebida por Tatiana foi flor e a matriz B(2X2) tal que b₁₁=1_, b₁₂=-1, b₂₁=2 e b₂₂ =1, então a matriz A é :

  

Resposta da questão 7:[B]

Com os dados do enunciado, pode-se escrever:

 

  

8. (Ueg 2016)  Um jovem vendedor recebe um salário mensal fixo de R$1000,00, mais uma comissão de R$50,00 por produto vendido. Se ele vender mais de 100 produtos, essa comissão passa a ser de R$100,00 por produto vendido. A função que descreve o salário mensal desse vendedor, na qual y  é o salário recebido (em reais) e x  a quantidade de produtos vendidos, é :

a) y = 1000+50x, se 0 ≤ x ≤ 100 e y = 1000 + 100x, se x > 100   

b) y = 1000+50x, se 0 ≤ x ≤ 100 e y = 100x, se x > 100      

c) y = 50x, se 0 ≤ x ≤ 100 e y = 100x, se x > 100      

d) y = 1000, se 0 ≤ x ≤ 100 e y = 1000 + 100x, se x > 100  

Resposta da questão 8:[A]

Montando-se o sistema, tem-se:

y = 1000+50x, se 0 ≤ x ≤ 100 e y = 1000 + 100x, se x > 100   

  

  

9. (Ueg 2016)  Um aluno terá que escrever a palavra PAZ utilizando sua caneta de quatro cores distintas, de tal forma que nenhuma letra dessa palavra tenha a mesma cor. O número de maneiras que esse aluno pode escrever essa palavra é :

a) 64    

b) 24    

c) 12    

d) 4    

Resposta da questão 9:[B]

O número de maneiras que esse aluno pode escrever essa palavra é igual ao arranjo de 4, 3 a 3. Ou seja: A_4,3 = 4.3.2 = 24

  

10. (Ueg 2016)  Uma montadora de carros oferece a seus clientes as seguintes opções na montagem de um carro: 2 tipos de motores (1.8 ou 2.0), 2 tipos de câmbios (manual ou automático), 6 cores (branco, preto, vermelho, azul, cinza ou prata) e 3 tipos de acabamento (simples, intermediário ou sofisticado). De quantas maneiras distintas pode-se montar esse carro?

a) 4  

b) 13  

c) 24  

d) 36  

e) 72  

Resposta da questão 10: [E]

O resultado será o produto do número de opções para cada item, ou seja:

2.2.6.3 = 72  

  

11. (Ueg 2016)  Pedro jogou dois dados comuns numerados de 1 a 6. Sabendo-se que o produto dos números sorteados nos dois dados é múltiplo de 3, a probabilidade de terem sido sorteados os números 3 e 4 é uma em :

a) 18    

b) 12    

c) 10    

d) 9  

  

Resposta da questão 11:[C]

Os possíveis produtos múltiplos de 3 dos números sorteados são:

- 3 (1 e 3 ou 3 e 1),  duas possibilidades,

- 6 (dados 6 e 1, 1 e 6, 2 e 3 ou 3 e 2), quatro possibilidades,

- 9 (dados 3 e 3),  uma possibilidade,

- 12 (dados 4 e 3, 3 e 4, 6 e 2 ou 2 e 6), quatro possibilidades,

- 15 (dados 3 e 5 ou 5 e 3), duas possibilidades,

- 18 (dados 3 e 6 ou 6 e 3), duas possibilidades,

- 24 (dados 6 e 4 ou 4 e 6), duas possibilidades,

- 30 (dados 6 e 5 ou 5 e 6), duas possibilidades,

- 36 (dados 6 e 6), uma possibilidade.

Portanto, há um total de 20 resultados possíveis nos quais o produto dos números sorteados é múltiplo de três. Logo, a probabilidade de terem sido sorteados os números 3 e 4 (ou 4 e 3)  é 2 em 20, ou uma em 10.  

12. (Ueg 2016)  Renata está grávida e realizará um exame que detecta o sexo do bebê. Se o exame detectar que é um menino, a probabilidade de ela pintar o quarto do bebê de azul é de 70%,  ao passo que de branco é de 30%. Mas, se o exame detectar que é uma menina, a probabilidade de ela pintar o quarto do bebê de rosa é de 60%  contra 40%  de pintar de branco. Sabendo-se que a probabilidade de o exame detectar um menino é de 50%,  a probabilidade da Renata pintar o quarto do bebê de branco é de :

a) 70%  

b) 50%  

c) 35%  

d) 30%  

e) 20%  

Resposta da questão 12: [C]

Probabilidade de nascer menino e pintar o quarto de branco : 50/100 . 30/100 = 15/100

Probabilidade de nascer menina e pintar o quarto de branco : 50/100 . 40/100 = 20/100.

Portanto, a probabilidade pedida será de: P = 15/100 + 20/100 = 35/100 = 35%

  

13. (Ueg 2016)  Uma circunferência de centro (-1,0) e raio 3 é interceptada por uma reta. Sabendo-se que os pontos (2/5,8/5) e (-√2,2+√2) pertencem à reta, a soma das coordenadas do eixo-x dos pontos de intersecção é :

a) -1   

b) 0   

c) 1   

d) √2   

Resposta da questão 13:C]

Calculando o coeficiente α da equação da reta, tem-se:

α = (√2 + 2 - 8/5) / (-√2 - 2/5) = (√2 + 2/5). (-√2 + 2/5) / (-√2 - 2/5) (-√2 + 2/5) →

α = (4/25 - 2) / (2 - 4/25) = -46/25 . 25/46 = -1

Calculando o coeficiente b da equação da reta, tem-se:

y = -x + b → 8/5 = -2/5 +b → b = 10/5 → b = 2

Portanto, a equação da reta será: y = - x + 2

A equação da circunferência é dada por: (x + 1)²  + y² - 9 = 0

Para encontrar os pontos de intersecção entre a reta e a circunferência basta substituir a equação da reta na equação da circunferência, ou seja:

(x + 1)²  + y² - 9 = 0 → (x + 1)²  + (-x + 2)² - 9 = 0

x²+ 2x + 1+ x²- 4x + 4 – 9 = 0 → x²- x – 2 = 0 → x = 2 ou x = - 1

Assim a soma das coordenadas do eixo x dos pontos de intersecção é 1.

  

14. (Ueg 2016)  A circunferência de centro (8,4) que tangencia externamente a circunferência x² + y² – 4x + 8y -16 = 0 possui raio igual a :

a) 16   

b) 10 

c) 8 

d) 6 

e) 4   

Resposta da questão 14: [E]

Desenvolvendo a equação:

x² + y² – 4x + 8y -16 = 0 → x² – 4x + 4 + y² + 8y + 16 = 16 + 16 + 4 →

( x – 2 )² + ( y + 4 )² = 36, temos então uma circunferência de centro C(2,4) e raio R = 6.

O raio r será a diferença entre a distância entre os centros P(8, 4) e C(2,-4) e o raio R = 6.

Portanto, r = √(8-2)²+(4-(-4))²  -  6 → r = 4

  

15. (Ueg 2016)  O trinômio do segundo grau y = (2m + 1)x² +4mx + m, em que m é um número real, é sempre positivo, se e somente se:

a) m>1/2   

b) 0<m<1/2   

c) m<1/2   

d) -1/2<m<0   

Resposta da questão 15:[B]

Para garantirmos que a equação do segundo grau tenha raízes positivas, seu delta deve ser menor que zero (∆<0) e seu coeficiente “a” deve ser positivo. Assim: 2m+1>0 → m > -1/2

∆ = (4m)² – 4.(2m+1).m = 16m² – 8m² – 4m =  8m² – 4m > 0→m>0 ou m<1/2

Assim, a condição para que o trinômio seja sempre positivo é 0 < m < 1/2

  

16. (Ueg 2016)  Alexandre Graham Bell foi o grande inventor da pipa tetraédrica, que pode ser construída com estruturas triangulares em diversos tamanhos, desde que mantidas suas propriedades. Para que a pipa possa subir ela não pode ser coberta em toda a sua estrutura, em cada uma delas cobre-se apenas dois lados. A Figura 1 mostra o início da construção de uma delas com quatro estruturas. A Figura 2 mostra a pipa já completa. Supondo-se que o triângulo já coberto que compõe cada lado da estrutura possui base igual a 3cm e altura 2cm, a área coberta de uma dessas pipas com 16 estruturas é :  

  

a) 96cm²   

b) 48cm²   

c) 40cm²   

d) 32cm²   

e) 24cm²   

Resposta da questão 16: [A]

Área de cada triângulo: A_∆ = 3.2/2 = 3

Cada tetraedro possui dois triângulos cobertos e a pipa possui 16 tetraedros em sua estrutura. Portanto, a área pedida será dada por:

A = 16 . 2 . A_∆ = 96cm²

  

17. (Ueg 2016)  Na divisão do polinômio 6x⁴ – 2x³ – 8x² +10x - 2 pelo divisor x² + 3x – 2, o resto multiplicado por 2 é :

a) -222x² + 252   

b) 444x² + 252      

c) -444x² + 252     

d)  222x² + 252      

e) -444x² - 252      

Resposta da questão 17:[C]

Efetuando a divisão, temos:

O dobro do resto será dado por 2.(-222x + 126) = -444x + 252  

  

18. (Ueg 2016)  A tabela a seguir apresenta o número de ônibus utilizados no transporte público de um município e o número de passageiros transportados num período de cinco dias.

Número de ônibus	Número de passageiros
47	1410
50	1400
48	1536
52	1352
49	1666

Os dados da tabela indicam que o número médio de passageiros transportados por ônibus nesse município durante esse período é 

a) superior a 30 e inferior a 40    

b) inferior a 30    

c) superior a 40 e inferior a 50    

d) superior a 50    

  

Resposta da questão 18:[B]

Calculando a média de passageiros por ônibus, têm-se:

 (1410 + 1400 + 1536 + 1352 + 1666)/(47 + 50 + 48 + 52 + 49) = 3682/123 < 30

  

19. (Ueg 2016)  Com a alta da inflação e para não repassar aos clientes o aumento dos gastos na produção de suco de laranja, um empresário decidiu que no próximo mês 10% do volume desse suco será composto por água, volume que atualmente é de apenas 4%. Se hoje são consumidos 10000 litros de água no volume de suco de laranja produzido, mantendo-se a mesma quantidade produzida, no próximo mês a quantidade de água consumida no volume desse suco será de :

a) 10000 litros    

b) 12500 litros    

c) 16000 litros    

d) 25000 litros    

  

Resposta da questão 19:[D]

Resolvendo utilizando a regra de três, tem-se:

Se 4% → 10000 entao 10% → x. Portanto x = 25000.

20. (Ueg 2016)  O gráfico a seguir representa a evolução do número de casos confirmados de zika vírus no período de novembro de 2015 a fevereiro de 2016, num município fictício. A porcentagem de aumento de casos de zika vírus no período de dezembro de 2015 a janeiro de 2016 é de :

a) 100%   

b) 150%   

c) 200%   

d) 250%   

e) 50%   

Resposta da questão 20:[B]

A variação pedida será dada por: (100 - 40) / 40 = 1,5 = 150%

  

21. (Ueg 2016)  Alterando-se as dimensões de uma caixa retangular de altura h, as dimensões da base serão multiplicadas por k e as da altura somado k, em que k é uma constante positiva e não nula. Logo, verifica-se que o volume da nova caixa será em relação à anterior :

a) k³ vezes maior   

b) k² + kh vezes maior   

c) k² + k³/h vezes maior   

d) k³ +√h/k vezes maior   

Resposta da questão 21:[C]

Comparando o novo volume com o volume antigo (original) pode-se escrever : V_antigo = a . b . h

V_novo = (h+k).ak.bk = abk².(h+k) = abhk² + abk³ = ab.(hk² + k³)

V_novo  = V_antigo .(hk² + k³)/h → V_novo  = V_antigo .(k² + k³/h)

  

22. (Ueg 2016)  A figura a seguir representa uma sequência lógica, na qual cada quadrado possui uma quantidade de quadradinhos pintados em seu interior. Se prosseguirmos dessa maneira verificaremos que o 8º quadrado possuirá :

 

a) abaixo de 1000 quadradinhos pintados.    

b) 6144 quadradinhos pintados.    

c) acima de 60000 quadradinhos pintados.    

d) 40320 quadradinhos pintados.    

Resposta da questão 22:[D]

A sequência de quadrados obedece a seguinte lógica:

Quadrado 1 → 1.1 = 1 quadrado preenchido

Quadrado 2 → 1.2 = 2 quadrados preenchidos

Quadrado 3 → 2.3 = 6 quadrados preenchidos

Quadrado 4 → 6.4 = 24 quadrados preenchidos

Assim se prosseguirmos dessa maneira verificaremos que o 8º quadrado possuirá:

Qudrado 5 → 24.5 = 120 quadrados preenchidos

Qudrado 6 → 120.6 = 720 quadrados preenchidos

Qudrado 7 → 720.7 = 5040 quadrados preenchidos

Qudrado 8 → 5040.8 = 40320 quadrados preenchidos

  

23. (Ueg 2016)  Na competição de skate a rampa em forma de U tem o nome de vert, onde os atletas fazem diversas manobras radicais. Cada uma dessas manobras recebe um nome distinto de acordo com o total de giros realizados pelo skatista e pelo skate, uma delas é a “180 allie frontside”, que consiste num giro de meia volta. Sabendo-se que 540⁰ e 900⁰ são côngruos a 180⁰, um atleta que faz as manobras 540 Mc Tuist e 900 realizou giros completos de :

a) 1,5 e 2,5 voltas respectivamente.   

b) 0,5 e 2,5 voltas respectivamente.   

c) 1,5 e 3,0 voltas respectivamente.   

d) 3,0 e 5,0 voltas respectivamente.   

e) 1,5 e 4,0 voltas respectivamente.   

  

Resposta da questão 23:[A]

540⁰ : 360⁰ = 1,5 voltas e 900⁰ : 360⁰ = 2,5 voltas

24. (Ueg 2016)  Sabendo-se que senx = 1/2 e que x é um ângulo do 1º quadrante, o valor da expressão sen4x – cos4x  é :

a) (√3-1)/2   

b) 1/2   

c) (√3+1)/2      

d) 2   

Resposta da questão 24:[C]

Se senx = 1/2 e está no 1º quadrante, então x = 30⁰. Logo, 4x = 2.60⁰, Desenvolvendo a equação dada, tem-se:

sen4x – cos4x  = sen(2.60⁰) - cos(2.60⁰) = 2sen60⁰cos60⁰- cos²60⁰ +sen²60⁰

2 . √3/2 . 1/2 - 1/4 + 3/4 = (2√3 + 2)/4 = (√3 + 1)/2

  

25. (Ueg 2016)  Os números de casos registrados de acidentes domésticos em uma determinada cidade nos últimos cinco anos foram: 100, 88, 112, 94 e 106. O desvio padrão desses valores é aproximadamente :

a) 3,6   

b) 7,2   

c) 8,5   

d) 9,0   

e) 10,0

Resposta da questão 25: [C]

Calculando a média aritmética, temos: m = (100+88+112+94+106)/5 = 100

E depois o desvio padrão:

d_p = √{(100-100)² +(100-88)² +(100-112)² +(100-94)² +(100-105)²}/5 =√72 ≈8,5