1. (Upf 2017) Seja an uma sequência de números reais cujo termo geral é an
= 1/4 – n, n ɛ N*. Qual das afirmações seguintes é verdadeira?
a) an é uma progressão aritmética
de razão – 1.
b) an é uma progressão
geométrica de razão 1/4.
c) an é uma progressão
geométrica de razão 4.
d) an não é uma progressão
(nem geométrica, nem aritmética).
e) an é simultaneamente uma
progressão aritmética e geométrica.
Resposta da questão 1:[A]
Calculando:
a1 = 1/4 – 1 = - 3/4 ; a1 = 1/4 – 2 = - 7/4 ; a1 = 1/4 – 3 = -11/4 →PA → r = -
1
Assim, a
alternativa correta é a letra [A].
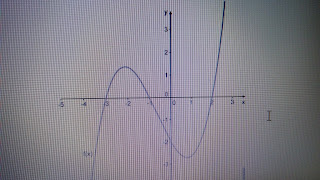
2. (Upf 2017) O gráfico a seguir representa a função polinomial f(x) = a(x - b)(x - c)(x
- d). O valor de a + b + c + d é:
a) -2
b) -5/3
c) 1/3
d) 7/3
e) 2
Resposta da questão 2:[B]
Das intersecções do gráfico, tem-se: f(x)
= a(x - b)(x - c)(x - d).
Com o eixo x (as raízes), f(x) = a(x + 3)(x
+ 1)(x - 2).
Com o eixo y, (0, - 2) ɛ f(x) → - 2 = a(0
+ 3)(0 + 1)(0 - 2)→ - 2 = - 6a → a = 1/3
Então a + b + c + d = 1/3 + (- 3) + (- 1) + 2 = 1/3 – 2 = - 5/3
3. (Upf 2017) Na figura, está representada uma roda gigante de um parque de diversões.
Um grupo de amigos foi andar nessa roda. Depois de todos estarem sentados nas
cadeiras, a roda começou a girar. Uma das meninas sentou na cadeira número 1,
que estava na posição indicada na figura, quando a roda começou a girar. A roda
gira no sentido contrário ao dos ponteiros dos relógios e leva um minuto para
dar uma volta completa.
Seja d a função que expressa a
distância da cadeira 1 ao solo, t minutos depois que a roda começou a girar. O
gráfico que representa parte da função d é:
Resposta da questão 3: [A]
A cadeira 1 nunca
toca o solo, logo a distância d nunca será zero (logo, o gráfico apresentado na
alternativa [B] está incorreto). A distância d aumenta nos primeiros 15
segundos, até a cadeira 1 atingir a posição 3. Depois, dos 15 aos 45 segundos a
distância d diminui (até a cadeira 1 atingir a posição 7) e então novamente
aumenta entre os segundos 45 e 60, até chegar na posição 1 (recomeçando o
ciclo). O único gráfico com estas características é o apresentado na
alternativa [A].
4. (Upf 2017) As portas de acesso de todos os quartos de certo hotel são identificadas
por meio de números ímpares formados com 3 elementos do conjunto S = {3, 4, 5,
6, 7, 8}. Nessas condições, é correto afirmar que o número máximo de quartos
desse hotel é:
a) 18
b) 27
c) 90
d) 108
e) 216
Resposta da questão 4:[D]
Número ímpar na terceira casa : 3, 5 e 7.
Portanto 6.6.3 = 108 possibilidades.
5. (Upf 2017) Considere os planos definidos por:
π1 : 2x – 3y + z = 1 ; π2 : - x + y + 2z = 0 e π3 : - 4x + 6y - 2z = - 2
Qual das figuras a seguir pode
descrever a posição relativa desses três planos no espaço?
Resposta da questão 5:[E]
Analisando π1 e π3
pode-se escrever π1 = π3. Logo, estes planos serão
coincidentes.
O plano π2 será
concorrente aos outros planos (não há proporcionalidade entre seus coeficientes
a, b e c, logo não serão nem coincidentes nem paralelos, podendo apenas ser
concorrentes).
A alternativa correta será a letra [E].
6. (Upf 2017) Considere as funções reais de variável real, definidas por:
f(x) = 1 + 3x – 2 e g(x) = logax
Sabe-se que, na representação gráfica
das funções, as curvas interceptam-se no ponto de abscissa 2. Dessa forma, o
valor de a é:
a) - √2
b) - 1/2
c) 1
d) 1/2
e) √2
Resposta da questão 6:[E]
Calculando: f(2) = g(2) → 1 + 32 – 2
= loga2 → 2 = loga2 → a2 = 2 → a = √2
7. (Upf 2017) Na figura a seguir, está representado, num referencial xy, um triângulo AOB.
Sabe-se que:
1. a semirreta AO é a bissetriz do 2º
quadrante;
2. a semirreta OB é a bissetriz do 1º
quadrante;
3. a ordenada do ponto B excede em 3
unidades a ordenada do ponto A;
4. a área do triângulo AOB é igual a 10.
As coordenadas dos pontos A e B são:
a) A(- 1/2 , 1/2)
e B(7/2 , 7/2)
b) A(- 1 , 1)
e B(4 , 4)
c) A(- 2 , 2)
e B(5 , 5)
d) A(- 3 , 3)
e B(6 , 6)
e) A(- 4 , 4)
e B(7 , 7)
Resposta da questão 7:[C]
Calculando:
S = (x√2).((x + 3)√2/2
= 10 → x√2.(x√2 + 3√2) = 20 → 2x2 + 6x – 20 = 0
x2 + 3x
– 10 = 0 → x' = - 5(não convém) ou x'' = 2
Então, A(- x, x)
= (- 2, 2) e B((x + 3),(x + 3)) = (5, 5)
8. (Upf 2017) No Brasil, os horários reservados à propaganda política de cada período
eleitoral são divididos entre os partidos e as coligações que tenham candidato
e representação na Câmara dos Deputados.
O TSE, seguindo instruções da lei,
tem adotado os seguintes critérios:
- o primeiro terço do tempo (dez
minutos) deve ser dividido igualitariamente entre todos os partidos/coligações com
candidatos, inclusive aqueles que não tenham representantes na Câmara dos
Deputados;
- os dois terços restantes (20
minutos) ficam reservados exclusivamente para partidos/coligações que possuam
representação na Câmara dos Deputados, dividindo-se o tempo de forma
proporcional ao número de representantes de cada partido/coligação.
Considere que João, Antônio, Luís e
Paulo se candidataram para concorrer a prefeito em um município do Rio Grande
do Sul.
O candidato João concorre pelo partido
PSDB; o candidato Antônio concorre pela coligação PT e PDT; o candidato Luís,
pelo PCdoB; e o candidato Paulo, pela coligação DEM e PSD.
Observe o extrato de tabela abaixo,
que apresenta o número de representantes de cada partido na Câmara de Deputados.
|
Partido
|
Bancada
|
Nome do
partido
|
|
PT
|
58
|
Partido dos
Trabalhadores
|
|
PSDB
|
50
|
Partido da
Social Democracia Brasileira
|
|
PSD
|
35
|
Partido
Social Democrático
|
|
DEM
|
27
|
Democratas
|
|
PDT
|
19
|
Partido
Democrático Trabalhista
|
|
PCdoB
|
11
|
Partido
Comunista do Brasil
|
|
(Disponível em:
http://www.camara.leg.br/Internet/Deputado/bancada.asp. Acesso em 10 set.
2016)
|
||
Assim, nos dias em que o programa
eleitoral exibe os programas dos candidatos a prefeito, o candidato Paulo
disporá de:
a) 2,5 min
b) 6,2 min
c) 7,5 min
d) 8,7 min
e) 16,2 mn
Resposta da questão 8:[D]
Calculando:
Total de candidatos = 4, tempo1/3
= 10/4 = 2,5 min
Paulo → DEM / PSD = 27 + 35 = 62
Total de deputados = 58 + 50 + 35 + 27 +
19 + 11 = 200
Tempo2/3 = 62.20/200 = 6,2 min
Tempo total = 2,5 + 6,2 = 8,7
min