1)
Considerem-se verdadeiras as proposições:
Toda criança é feliz.
Existem pessoas que usam
óculos e não são felizes.
Nessas condições, é
correto concluir-se:
01) Nenhuma criança usa óculos.
02) As pessoas que não usam óculos são
felizes.
03) Todas as crianças que usam óculos são felizes.
04)Existem crianças que usam óculos e não
são felizes.
05)Existem crianças que não usam óculos e
que não são felizes.
Vejamos :
Se, Toda criança é feliz é uma proposição verdadeira então,
necessariamente, Todas as crianças que usam óculos são felizes, também será
verdadeira.
2)
No dia 1º de março de 2015, dois médicos
amigos, M e N, montaram uma
Clínica de Assistência ao Idoso – CAI – com uma capital social de dois milhões
de reais, devendo, cada um deles, participar com um milhão de reais. Quando
abriram a empresa, M integralizou sua quota e N, apenas contribuiu com
R$ 700.000,00, completando-a após 5 meses. Ao proceder o balanço, em 31 de
dezembro do mesmo ano, apuraram um lucro de 740.000,00 reais, cabendo,
pois, em milhares de reais, para M e para N, respectivamente:
Clínica de Assistência ao Idoso – CAI – com uma capital social de dois milhões
de reais, devendo, cada um deles, participar com um milhão de reais. Quando
abriram a empresa, M integralizou sua quota e N, apenas contribuiu com
R$ 700.000,00, completando-a após 5 meses. Ao proceder o balanço, em 31 de
dezembro do mesmo ano, apuraram um lucro de 740.000,00 reais, cabendo,
pois, em milhares de reais, para M e para N, respectivamente:
01) 340 e 400
02) 350 e 390
03) 360 e 380
04) 370 e 370
05) 400 e 340
Vejamos :
M entrou com um milhão em 1º de março e N entrou com R$ 700.000,00
em 1º
de março e R$ 300.000,00 em 31 de julho.
de março e R$ 300.000,00 em 31 de julho.
Portanto M está para R$1.000.000,00 e 10 meses assim como N está
para
R$ 700.000,00 em 5 meses e R$ 1.000.000,00 em 5 meses.
R$ 700.000,00 em 5 meses e R$ 1.000.000,00 em 5 meses.
Apuraram um lucro de 740 milhões de reais, em 31 dezembro.
A situação apresentada caracteriza uma divisão proporcional.
M/1000.10 = N/(700x5 + 1000x5) = (M + N)/ (1000 + 700x5 + 1000x5)
M/10000 = N/(3500 + 5000) = 740/(18000 + 8500) → M/10000 = N/8500 =
740/18500
M/100 = N/85 = 740/185 → M/100 = 740/185 e N/85 = 740/185 →
M = 100. 740/185 = 400 e N = 85.740/185 = 340
3) Em um bairro de determinada cidade, uma
população de 400 habitantes foi
submetida a exames para detectar portadores de Dengue e de Anemia.
Dos resultados obtidos, observou-se que:
submetida a exames para detectar portadores de Dengue e de Anemia.
Dos resultados obtidos, observou-se que:
80% das pessoas que possuíam Dengue também possuíam Anemia
0,50 das pessoas com Anemia
também possuíam Dengue
0,55 das pessoas não possuía nem Dengue nem Anemia
Com base nessas informações, pode-se concluir que, das
400 pessoas
examinadas, o número correspondente à porcentagem das pessoas que
possuíam apenas Dengue é igual a:
examinadas, o número correspondente à porcentagem das pessoas que
possuíam apenas Dengue é igual a:
01) 88
02) 100
03) 112 QUESTAO INCOERENTE !
04) 124
05) 136
Vejamos : Dengue = y + z e
Anemia = z + w
Com auxílio do diagrama de Venn, podemos escrever: x + y + z + w =
400
80% das pessoas que possuíam Dengue também possuíam Anemia→z = 80%
de (z+y)
z = 0,8. (z + y) → z = 0,8z + 0,8y → 0,2z = 0,8y → z = 4y
0,50 das pessoas com Anemia também possuíam Dengue → z = 0,5.(z + w)
→
z = 0,5z + 0,5w → 0,5z = 0,5w → z = w
0,55 das pessoas não possuía nem Dengue nem Anemia → x = 0,55 de 400
= 220
Portanto : x + y + z + w = 400 → 220 + y + z +
w = 400 → y + z + w = 180 →
y + 4y + 4y = 180 → 9y = 180 → y = 20
Esta questão
apresenta uma incoerência, veja: o número
correspondente à porcentagem das pessoas que possuíam
apenas Dengue é igual a 20 de 400 = 5%
correspondente à porcentagem das pessoas que possuíam
apenas Dengue é igual a 20 de 400 = 5%
4)
Participando de um Congresso, compareceram
900 profissionais da Área,
sendo 75% constituído de Especialistas. Se n Especialistas se retirassem,
o percentual deles, em relação ao total de profissionais, inicialmente presentes,
cairia para 50%, então pode-se concluir que o valor preciso de n é:
sendo 75% constituído de Especialistas. Se n Especialistas se retirassem,
o percentual deles, em relação ao total de profissionais, inicialmente presentes,
cairia para 50%, então pode-se concluir que o valor preciso de n é:
01) 225
02) 275
03) 300
04) 450
05) 675
Vejamos :
Participando de um Congresso, compareceram 900 profissionais, sendo
75% de 900 = 675 especialistas.
Se n especialistas se retirassem, o percentual deles, em relação ao
total de profissionais, inicialmente presentes, cairia para 50% → (675 - n) =
50% de 900
675 – n = 0,5.900 → 675 – n = 450 → 675 – 450 = n → n = 225
675 – n = 0,5.900 → 675 – n = 450 → 675 – 450 = n → n = 225
5) Para determinadas pessoas que possuem
dieta diferenciada ou querer
perder peso, existe uma grande variedade de alimentos indicados nessas
categorias, como produtos light e/ou diet. Considerando-se que um alimento
light contém, no máximo, um terço das calorias da sua versão normal, ou
contém menos da metade da quantidade da gordura contida em sua
versão normal, tem-se que se certo alimento contém 84 calorias e 7,0g
de gordura, então a sua versão light contém:
perder peso, existe uma grande variedade de alimentos indicados nessas
categorias, como produtos light e/ou diet. Considerando-se que um alimento
light contém, no máximo, um terço das calorias da sua versão normal, ou
contém menos da metade da quantidade da gordura contida em sua
versão normal, tem-se que se certo alimento contém 84 calorias e 7,0g
de gordura, então a sua versão light contém:
01) 38 calorias e 3,5g de gordura
02) 38 calorias, no mínimo, e menos de 2,0g
de gordura
03) 28 calorias, no máximo, ou menos de 3,5g de gordura
04) 28 calorias, no mínimo, ou mais de 3,5g
de gordura
05) 28 calorias, no máximo, e menos de 2,0g
de gordura
Vejamos :
Caloria de um alimento ligth ≤ 1/3 da caloria de uma versão normal →
x ≤ 1/3 de 84 →x ≤ 28 calorias
x ≤ 1/3 de 84 →x ≤ 28 calorias
Gordura de um alimento ligth < 1/2 da gordura de uma versão
normal →
x < 1/2 de 7,0 → x < 3,5g de gordura
x < 1/2 de 7,0 → x < 3,5g de gordura
6) Considere n o cardinal de an
= -250, na progressão aritmética (-2, -6, -10,...)
e s, a soma dos 9 primeiros termos da progressão geométrica (3, 6, 12, 24, ...).
Desse modo, é correto afirmar que o valor de s – n é:
e s, a soma dos 9 primeiros termos da progressão geométrica (3, 6, 12, 24, ...).
Desse modo, é correto afirmar que o valor de s – n é:
01) 1596
02) 1470
03) 1246
04) 735
05) 511
Vejamos :
Sobre a PA (-2, -6, -10,...), an = a1 + (n -
1)r → - 250 = - 2 + (n - 1).(- 4) → - 248 = - 4n + 4
4n = 248 + 4 → 4n = 252 → n = 63
Sobre a PG
(3, 6, 12, 24, ...), Sn = a1.(qn - 1)/(q - 1)
→ S9 = 3.(29 - 1)/(2 - 1) →
S9
= 3.(512 - 1) → S9 = 3.511 → S9 = 1533
Portanto S9
– n = 1533 – 63 = 1470
7) Se (3/4)x = 256/81e (y/3)2
= 729, para x e y números reais, y > 0, então o valor
de y + 3x é:
de y + 3x é:
01) 33
02) 48
03) 56
04) 69
05) 77
Vejamos :
Se (3/4)x = 256/81 → (3/4)x = (4/3)4
→ (3/4)x = (3/4)-4 → x = - 4
Se (y/3)2 = 729 → y/3 = √729, y > 0,
→ y/3 = 33 → y = 81
Portanto, y + 3x = 81 + 3.(- 4) = 81 – 12 = 69
8) Buscando incentivar a participação e
estimular a criatividade, o
Departamento de Relações Humanas, (RH), de uma Empresa, promoveu
um sorteio entre seus funcionários, de modo que o número n sorteado
tivesse quatro algarismos distintos e não nulos, isto é, n = pqrs, e que
o possuidor do número sorteado n só pudesse receber o prêmio se
soubesse calcular o seu valor. Além disso, sabe-se que o valor do prêmio
era igual à soma de todos os números de quatro algarismos obtidos,
permutando-se os algarismos de n. nessas condições, para
S = p + q + r + s, pode-se afirmar que o valor do prêmio, em função de S, é:
Departamento de Relações Humanas, (RH), de uma Empresa, promoveu
um sorteio entre seus funcionários, de modo que o número n sorteado
tivesse quatro algarismos distintos e não nulos, isto é, n = pqrs, e que
o possuidor do número sorteado n só pudesse receber o prêmio se
soubesse calcular o seu valor. Além disso, sabe-se que o valor do prêmio
era igual à soma de todos os números de quatro algarismos obtidos,
permutando-se os algarismos de n. nessas condições, para
S = p + q + r + s, pode-se afirmar que o valor do prêmio, em função de S, é:
01) 3030S
02) 3333S
03) 6060S
04) 6666S
05) 9090S
Vejamos :
... todos os números de quatro algarismos obtidos, permutando-se os
algarismos de n, ou seja 4! = 4.3.2.1 = 24 possibilidades.
algarismos de n, ou seja 4! = 4.3.2.1 = 24 possibilidades.
Vamos imaginar as 24 possibilidades, exemplo n = 1234
1234 1243 1324 1342 1423 1432
2134 2143
2314 2341
2413
2431
3124 3142 3214
3241
3412
3421
4123 4132 4213 4231 4312 4321
Note que cada algarismo aparece 6 vezes em cada ordem, ou seja, 6
na milhar, 6 na centena, 6 na dezena e 6 na unidade.
na milhar, 6 na centena, 6 na dezena e 6 na unidade.
Sendo assim, o valor do premio será P = (6.1000 + 6.100 + 6.10 +
6).(1 + 2 + 3 + 4) →
P = (6000 + 600 + 60 + 6).10 → P = 66660
Generalizando para n =
pqrs, teríamos P = (6.1000 + 6.100 + 6.10 + 6).(p + q + r + s) →
P = (6.1000
+ 6.100 + 6.10 + 6).S → P = 6666S
9) Uma panificadora utiliza fermento
biológico no processo de industrialização
de seus alimentos, de modo que seus produtos têm, a cada hora, o volume
V aumentado em 20%. Nessas condições, é correto afirmar que, em 2 horas,
o volume de determinado alimento:
de seus alimentos, de modo que seus produtos têm, a cada hora, o volume
V aumentado em 20%. Nessas condições, é correto afirmar que, em 2 horas,
o volume de determinado alimento:
01) cresceu pouco menos da metade
02) alcançou 1,8V
03) dobrou
04) atingiu 2,5V
05) triplicou
Vejamos :
Volume V aumentado em 20% a
cada hora → V = V0.1,2t.
Em duas horas → V = V0.1,22 → V = V0.1,44
→ Aumentou em 44%
10) Em um espaço amostral E, considere-se a ocorrência de
duas epidemias
como dois eventos independentes, M e N. Sabendo-se que a probabilidade
de ocorrer M é P(M) = 40% e que a probabilidade de ocorrer a união de M
com N é P(MUN) = 80%, pode-se concluir que a probabilidade de ocorrer o
evento N é de:
como dois eventos independentes, M e N. Sabendo-se que a probabilidade
de ocorrer M é P(M) = 40% e que a probabilidade de ocorrer a união de M
com N é P(MUN) = 80%, pode-se concluir que a probabilidade de ocorrer o
evento N é de:
01) 1/2
02) 2/3
03) 3/4
04) 4/5
05) 5/6
Vejamos :
Dois eventos, M e N, de um
mesmo espaço amostral são independentes
quando a probabilidade de
que eles ocorram simultaneamente for
igual ao
produto de suas
probabilidades individuais, ou seja, M e N serão
independentes quando: P(M ∩
N) = P(M).P(N) → P(M ∩ N) = 40%.P(N) →
P(M ∩ N) = 40/100 . P(N) →
P(M ∩ N) = 2/5.P(N)
Como P(MUN)
= P(M) + P(N) - P(M∩N), entao 80% = 40% + P(N) - 2/5.P(N) →
80% - 40% =
(1 - 2/5).P(N) → 40% = (1 - 2/5).P(N) → 2/5 = (1 -
2/5).P(N) →
2/5 = (3/5).P(N)
→ (2/5)/(3/5) = PN → PN = 2/3
11)
A balança comercial e financeira vem
sofrendo, com frequência, alterações
cambiais nesses últimos messes, quando o valor das moedas comerciais tem
oscilado bastante. Admitindo-se que o euro, por exemplo, variou de valores,
conforme a seguinte listagem: 3,78; 3,74; 3,67; 3,72; 3,65; 3,70; 3,69; 3,75.
Pode-se concluir que a mediana do valor do euro, neste período foi igual a:
cambiais nesses últimos messes, quando o valor das moedas comerciais tem
oscilado bastante. Admitindo-se que o euro, por exemplo, variou de valores,
conforme a seguinte listagem: 3,78; 3,74; 3,67; 3,72; 3,65; 3,70; 3,69; 3,75.
Pode-se concluir que a mediana do valor do euro, neste período foi igual a:
01) 3,66
02) 3,68
03) 3,70
04) 3,71
05) 3,73
Vejamos :
Colocando os valores em ordem crescente, 3,65 ; 3,67; 3,69; 3,70;
3,72; 3,74;
3,75; 3,78 a mediana é a média aritmética dos valores centrais : (3,70 + 3,72)/2 = 3,71
3,75; 3,78 a mediana é a média aritmética dos valores centrais : (3,70 + 3,72)/2 = 3,71
12) Dez amigos resolveram fazer uma viagem
em determinada época do ano
e, para concretizar a ideia, abriram uma conta poupança com depósito individual
mensal de R$200,00, a ser mensalmente corrigido pelo fator 1,02 , durante dez
messes. Admitindo-se utilizar (1,02)5 = 1,1040 (quatro algarismos na parte
decimal), em todos os cálculos, pode-se concluir que, no final de dez messes,
cada um deles havia poupado para a viagem o valor, em reais, de:
e, para concretizar a ideia, abriram uma conta poupança com depósito individual
mensal de R$200,00, a ser mensalmente corrigido pelo fator 1,02 , durante dez
messes. Admitindo-se utilizar (1,02)5 = 1,1040 (quatro algarismos na parte
decimal), em todos os cálculos, pode-se concluir que, no final de dez messes,
cada um deles havia poupado para a viagem o valor, em reais, de:
01) 2072,00
02) 2144,00
03) 2188,00
04) 2216,00
05) 2260,00
Vejamos :
Como a
conta deverá ser mensalmente corrigido
pelo fator 1,02, então
trata-se de uma progressão geométrica de a1 = 200 e razão q = 1,02.
trata-se de uma progressão geométrica de a1 = 200 e razão q = 1,02.
Pode-se concluir que, no final de dez messes, Sn = a1.(qn
- 1)/(q - 1) →
S10 = 200.(1,0210 - 1)/(1,02 - 1) → S10
= 200.((1,025)2 - 1)/0,02 →
S10 = 200.((1,104)2 - 1)/0,02
S10 = 200.((1,104)2 - 1)/0,02
S10 = 200.(1,2188 - 1)/0,02 → S10 = 200.0,2188/0,02
→ S10
= 2188,00
13) Considerando-se as funções p(x) = D.cos(Kx),
com D, k constantes reais,
0 < k < π/2,
x ∈ R,
p(0) = 2, p(1) = √3, e h(x) = 12 – p(x), tem-se que o valor de h(6) é:
01) 0
02) 2
03) 6
04) 10
05) 14
Vejamos :
Sendo p(x)
= D.cos(Kx), entao :
p(0) = 2 →
D.cos(k.0) = 2 → D.cos(0) = 2 → D.1 = 2 → D = 2
p(1) = √3 →
2.cos(k.1) = √3 → 2.cosk = √3 → cosk = √3/2, 0 < k < π/2, k = π/6
Portanto
p(x) = 2.cos(πx/6) e h(x) = 12 - 2.cos(πx/6)
Finalmente
h(6) = 12 - 2.cos(π.6/6) → h(6) = 12 - 2.cosπ → h(6) = 12 - (- 2) = 14
14) Admitindo-se que os números complexos, z e w (conjugado de z), são
tais que os pontos de intersecção dos lugares geométricos que representam
as soluções das equações z . w = 9 e z2 = (w)2 são vértices de um quadrilátero,
pode-se afirmar que o valor da área, em u. a., desse quadrilátero, é:
tais que os pontos de intersecção dos lugares geométricos que representam
as soluções das equações z . w = 9 e z2 = (w)2 são vértices de um quadrilátero,
pode-se afirmar que o valor da área, em u. a., desse quadrilátero, é:
01) 3
02) 6
03) 9
04) 12
05) 18
Vejamos :
Sendo os números complexos, z e w (conjugado de z),
z = a + bi e w = a – bi
Se z . w = 9 → (a + bi).(a
- bi) = 9 → a2 – b2i2 = 9 → a2 + b2
= 9
Se z2 = (w)2 → (a
+ bi)2 = (a - bi)2
→ a2 + 2abi + b2i2 = a2 - 2abi + b2i2
→ 2abi = - 2abi
4abi = 0 → 4ab = 0 → a = 0 ou b = 0.
Se a = 0 e a2 + b2 = 9 → b2 = 9 → b
= 3 ou b = - 3 → Z1 = 3i ou Z2 = - 3i
Se b = 0 e a2 + b2 = 9 → a2 = 9 → a
= 3 ou a = - 3 → Z3 = 3 ou Z4 = - 3
Como o quadrilátero formado é um quadrado de diagonal 6 u.c., e esta
diagonal mede d = lado√2, então o lado = d√2 = 6/√2 = 6√2/2 = 3√2 u.c.
diagonal mede d = lado√2, então o lado = d√2 = 6/√2 = 6√2/2 = 3√2 u.c.
Finalmente a área será igual a A = l2 = (3√2)2
= 18
u.a.
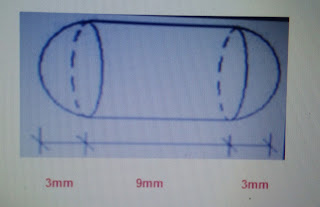
15) Considere-se que:
Cápsulas de formato cilíndrico e extremidades hemisféricas, contém
determinado medicamento em microesferas de 1,0mm de diâmetro;
determinado medicamento em microesferas de 1,0mm de diâmetro;
O comprimento total de cada cápsula mede 15mm, e o diâmetro de cada
hemisfera mede 6mm;
hemisfera mede 6mm;
É correto afirmar que o número máximo de microesferas que
cabem no interior
de cada cápsula, admitindo-se desprezíveis os espaços entre elas, é:
de cada cápsula, admitindo-se desprezíveis os espaços entre elas, é:
01) 500
02) 681
03) 702
04) 765
05) 804
Vejamos :
Cada
cápsula é formada por um cilindro, de altura 9 mm e raio da base
3 mm e duas hemisferas (V = 2πr3/3) de raio 3 mm, como indica a figura.
3 mm e duas hemisferas (V = 2πr3/3) de raio 3 mm, como indica a figura.
Portanto
seu volume será dado por V = πr2h + 2.2πr3/3 → V = π.32.9
+ 4π33/3
V = 81π + 36π
→ V = 117π mm3
Como o
volume de uma microesfera é V = 4πr3/3 → V = 4π(1/2)3/3 →
V = π/6 mm3
O número máximo de microesferas que cabem no interior de cada
cápsula
poderá ser obtido através do quociente entre o volume da cápsula e o da
microesfera, n0 = (117π)/(π/6) = 702
poderá ser obtido através do quociente entre o volume da cápsula e o da
microesfera, n0 = (117π)/(π/6) = 702