Questão 1)
Madalena possui um livro com diversas figuras geométricas
planificadas. Três dessas figuras são mostradas a
seguir.
Após
recortar essas figuras do livro e fazer as devidas colagens, ela obtém as
figuras espaciais
a)
tetraedro, octaedro e hexaedro.
b) paralelepípedo,
tetraedro e octaedro.
c)
octaedro, prisma e hexaedro.
d) pirâmide,
tetraedro e hexaedro.
e) pirâmide pentagonal,
prisma pentagonal e hexaedro.
Resolução
Alternativa correta: E
Após montar as figuras
que estão planificadas, obtemos, na sequência, uma pirâmide pentagonal, um
prisma pentagonal e um hexaedro.
Questão 2)
Suponha que, na escultura do artista Emanoel Araújo, mostrada
na figura a seguir, todos os prismas numerados em algarismos romanos são
retos, com bases triangulares, e que as faces laterais do poliedro II
são perpendiculares à sua própria face superior, que, por sua vez, é
um triângulo congruente ao triângulo base dos prismas. Além disso,
considere que os prismas I e III são perpendiculares ao prisma IV e ao
poliedro II.
Disponível
em: www.escritosriodearte.com.br. Acesso em: 28 jul. 2009.
Imagine
um plano paralelo à face α
do prisma I, mas que passe pelo ponto P pertencente à aresta do poliedro
II, indicado na figura. A interseção desse plano imaginário com a
escultura contém
a)
dois triângulos congruentes com lados correspondentes paralelos.
b)
dois retângulos congruentes e com lados correspondentes paralelos.
c)
dois trapézios congruentes com lados correspondentes perpendiculares.
d)
dois paralelogramos congruentes com lados correspondentes paralelos.
e)
dois quadriláteros congruentes com lados correspondentes perpendiculares.
Resolução
Alternativa correta: A
Dois triângulos
congruentes com lados correspondentes paralelos, pois os primas II e IV
são paralelos.
Questão 3)
Corta-se
um cubo ABCDEFGH por um
plano ortogonal às faces: ABCD e
EFGH que contém os pontos médios
I e J das arestas CD e BC e elimina-se, em seguida, o
prisma IJCLKG, obtendo-se o
prisma ABJIDEFKLH.
A
planificação da superfície do prisma resultante ABJIDEFKLH, corresponde à
figura
Resolução
Alternativa correta: E
Sejam CA e CB respectivamente,
as médias do custo por quilômetro nas cidades A e B . Assim,
CA – CB = 2,05 + 3,45/6 –
1,9 – 3,6/6 ≈ 0,13.
Questão 4)
Um quebra-cabeça é composto por apenas três peças que, quando
encaixadas corretamente, formam o retângulo da figura.
Assinale
a alternativa que apresenta as três peças que permitem montar esse
quebra-cabeça.
Resolução
Alternativa correta: D
Observe que as peças da alternativa D montam
o quebra-cabeça.
Questão 5)
Nas
figuras seguintes, pode-se traçar eixos imaginários de forma que elas
fiquem divididas em duas partes idênticas.
Isso
se deve por causa da
a)
rotação das figuras.
b)
simetria das figuras.
c)
translação das figuras.
d)
homotetia das figuras.
e)
deformação das figuras.
Resolução
Alternativa correta: B
As figuras possuem eixo
de simetria como mostrado a seguir.
Questão 6)
Em
uma atividade de sala, o professor Robério planificou um cubo e escreveu
nas faces os numerais de 1 a 6 conforme a figura a seguir.
De
acordo com a ilustração,
a) a soma dos
numerais das faces opostas é sempre um numeral par.
b) o produto dos numerais
das faces opostas é sempre um numeral par.
c) a soma dos
numerais das faces opostas é sempre um divisor de 3.
d) a soma dos
numerais das faces não opostas à face 1 é um numeral múltiplo de 3.
e) o produto dos
numerais das faces não opostas à face 6 é igual a 20.
Resolução
Alternativa correta: D
Montando o cubo que
está planificado, obtém-se a figura a seguir:
Observe que a face 6 é
oposta à face 3, a face 4 é oposta à face 2 e a face 5 é oposta à face 1.
Então, as faces não opostas à face 1 são 2, 3, 4 e 6, cuja soma é 15, que
é um numeral múltiplo de 3.
Questão 7)
Uma
pedra preciosa que possui o formato de octaedro regular está guardada no
interior de uma caixa transparente em formato de cubo com 4 cm de aresta
conforme a figura a seguir.
Os
vértices da pedra preciosa coincidem com os centros das faces do cubo. O
volume dessa pedra é
a) 64/3 cm3
b) 32/3 cm3
c) 16/3 cm3
d) 8/3 cm3
e) 4/3 cm3
Resolução
Alternativa correta: B
Observe a figura.
Questão 8)
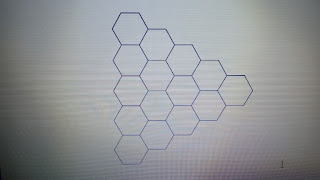
Paulo
desenhou no quadro de sua sala de aula o seguinte padrão de hexágonos
regulares.
Guilherme,
seu filho mais velho, ligou os centros de todos os pares de hexágonos
vizinhos. Qual padrão foi obtido por todas as ligações de Guilherme?
Resolução
Alternativa correta: C
Ligando os centros de
quaisquer dois hexágonos vizinhos, obtém-se a figura a seguir.
Na qual, o padrão
obtido após retirarmos os hexágonos é:
Questão 9)
Para montar um cubo, Lílian recortou um pedaço
de cartolina branca e pintou de cinza algumas partes, conforme mostra
a figura.
Qual
das figura abaixo representa o cubo construído por Lílian?
Resolução
Alternativa correta: C
Ao montar o cubo, a
face branca e a face cinza ficam opostas. Logo, as alternativas A e B
estão excluídas. As alternativas D e E estão excluídas também, pois no
cubo não podem aparecer um retângulo branco e outro cinza com um lado
menor em comum. Resta, então a alternativa C.
Questão 10)
João propôs um desafio a Bruno, seu colega de classe: ele
iria descrever um deslocamento pela pirâmide a seguir e Bruno deveria
desenhar a projeção desse deslocamento no plano da base da pirâmide.
O
deslocamento descrito por João foi: mova-se pela pirâmide, sempre em linha
reta, do ponto A ao ponto E, a seguir do ponto E ao ponto M, e depois de M
a C. O desenho que Bruno deve fazer é
Resolução
Alternativa correta: C
Questão 21)
Um
foguete foi lançado do marco zero de uma estação e após alguns segundos
atingiu a posição (6, 6, 7) no espaço, conforme mostra a figura. As
distâncias são medidas em quilômetros. medidas em quilômetros.
Considerando
que o foguete continuou sua trajetória, mas se deslocou 2 km para frente
na direção do eixo-x, 3 km para trás na direção do eixo-y, e 11 km para
frente, na direção do eixo-z, então o foguete atingiu a posição
a) (17, 3, 9).
b) (8, 3, 18).
c) (6, 18, 3).
d) (4, 9, - 4).
e) (3, 8, 18).
Resolução
Alternativa correta: B
Solução: Seguindo os deslocamentos
descritos, podemos seguir a seguinte sequência
( 6, 6, 7 ) → ( 6+2, 6-3, 7+11 ) → ( 8, 3,
18 )
Questão 22)
O
gráfico a seguir mostra o início da trajetória de um robô que parte do ponto A
(2, 0), movimentando-se para cima ou para a direita, com velocidade de uma
unidade de comprimento por segundo, no plano cartesiano. O
gráfico exemplifica uma trajetória desse robô, durante 6 segundos.
Supondo
que esse robô continue essa mesma trajetória, qual será sua coordenada após 18
segundos de caminhada, contando o tempo a partir do ponto A?
a)
(0, 18)
b)
(18, 2)
c)
(18, 0)
d)
(14, 6)
e)
(6, 14)
Resolução
Alternativa correta: D
Seguindo o padrão do
caminho mostrado na figura do texto-base, a trajetória que o robô seguirá está
representada na figura a seguir. Vê-se que ele para no ponto de coordenadas (14, 6).
Questão 23)
João
mora em Brasília, a capital do Brasil. Sua residência fica na SQN 202, e seu
trabalho na SQN 204, ele percorre diariamente o trajeto indicado no mapa a
seguir, seguindo de A até B.
Orientando-se
pelos pontos cardeais desenhados no mapa, qual é a orientação da trajetória que
João deve seguir desde sua residência até seu local de trabalho?
a) Oeste, Norte, Oeste
b) Oeste, Leste, Oeste
c)
Leste, Leste, Norte, Oeste
d)
Leste, Sul, Leste, Norte, Oeste
e) Oeste, Sul, Oeste, Norte, Oeste
Resolução
Alternativa correta: D
A orientação da
trajetória é leste, sul, leste, norte e oeste.
Questão 24)
O
Museu do Louvre, localizado em Paris, na França, é um dos museus mais visitados
do mundo. Uma de suas atrações é a Pirâmide de Vidro, construída no final da década
de 1980. A seguir tem-se, na Figura 1, uma foto da Pirâmide de Vidro do Louvre
e, na Figura 2, uma pirâmide reta de base quadrada que a ilustra.
Considere
os pontos A, B, C, D como na Figura 2. Suponha que alguns reparos devem ser
efetuados na pirâmide. Para isso, uma pessoa fará o seguinte deslocamento: 1)
partir do ponto A e ir até o ponto B, deslocando-se pela aresta AB; 2) ir de B
até C, deslocando-se pela aresta que contém esses dois pontos; 3) ir de C até
D, pelo caminho de menor comprimento; 4) deslocar-se de D até B pela aresta que
contém esses dois pontos.
Disponível
em: http://viagenslacoste.blogspot.com. Acesso em: 29 fev. 2012.
A
projeção do trajeto da pessoa no plano da base da pirâmide é melhor
representada por
Resolução
Alternativa correta: C
Sejam B’, C’ e D’ as
projeções, respectivamente, dos pontos B, C e D sobre a base da pirâmide. A
projeção do ponto A coincide com este, pois está na base da pirâmide.
Observando a figura a seguir, conclui-se que a melhor representação
é a da alternativa C.
Questão 25)
Observe o ponto P na imagem a seguir. Ele é o ponto da roda da bicicleta
que faz contato com o piso plano.
Qual
desenho representa parte da trajetória percorrida pelo ponto P quando a
ciclista se movimenta sobre o piso plano?
Resolução
Alternativa correta: B
É necessário
inicialmente, analisar a posição do ponto P a cada intervalo de uma unidade de
tempo. Para isso, observe a seguinte figura:
O conjunto de todos os
pontos P destacados corresponde à trajetória percorrida por esse ponto quando a
ciclista se desloca ao longo de um piso plano. Essa curva, denominada cicloide,
é mostrada a seguir.
Questão 26)
Antigamente, os pneus de carros possuíam uma câmara de ar interna, como
a da figura seguinte.
Esse sólido geométrico é denominado toroide e pode ser obtido pela
rotação completa de uma figura plana em torno de um eixo de rotação, como
mostrado a seguir.
Eixo de rotação
Qual
figura plana pode ser rotacionada em torno desse eixo para gerar o toroide?
a)
Triângulo.
b)
Semicírculo.
c) Quadrado.
d)
Icoságono.
e)
Círculo.
Resolução
Alternativa correta: E
A figura plana que pode
ser rotacionada em torno do eixo para gerar o toroide é o círculo. Veja a ilustração.
Questão 27)
As torres Puerta de Europa, também conhecidas por Torres KIO,
são duas torres inclinadas uma contra a outra em Madri, Espanha. A
inclinação das torres é de 15° com a vertical e ambas têm altura de 114 m,
com 26 andares.
Essas
torres apresentam a forma de
a) pirâmides
oblíquas de base triangular.
b) pirâmides
oblíquas de base quadrada.
c) troncos de
pirâmides oblíquas de base quadrada.
d) prismas oblíquos
de base quadrangular.
e) prismas oblíquos
de base decagonal.
Resolução
Alternativa correta: D
As torres representam
prismas oblíquos de base quadrangular, conforme a figura a seguir.
Questão 28)
O
Fast-Food
Refeição rápida ou fast-food
(inglês) é o nome genérico dado ao consumo de alimentos que pode ser
feito num intervalo pequeno de tempo. Este tipo de alimentação engloba
essencialmente: sanduíches, pizzas, refrigerantes, hambúrgueres e
batatas fritas e é muito apreciado pela maioria das crianças e jovens.
Contudo, também os adultos têm vindo a aderir ao fast-food devido ao ritmo de vida acelerado que faz com que o
tempo seja escasso até para comer.
Disponível
em:
<http://efa-espombal.blogspot.com.br/2007/07/o-fast-food-turma-b.html>.
Acesso em 27 abr. 2012.
A figura mostra um prato preparado em estabelecimentos de alimentos fast-food.
Uma
forma geométrica espacial identificada dentre os alimentos dessa figura é
a) cone.
b) pirâmide.
c) prisma.
d) tronco de
pirâmide.
e) tronco de cone.
Resolução
Alternativa correta: E
A figura mostra uma
porção de arroz que possui o formato de um tronco de cone.
Questão 29)
Alguns supermercados têm usado um prisma de madeira para
separar, no caixa, as compras dos clientes que já foram registrados.
Suponha
que esse prisma seja triangular regular maciço e que a aresta da base
tenha 2 cm e a altura 20 cm. Usando √3 ≅1,7, o volume desse
prima, em cm³, é
a) 34 cm³.
b) 33 cm³.
c) 32 cm³.
d) 31 cm³.
e) 30 cm³.
Resolução
Alternativa correta: A
O referido prisma possui base triangular
regular. Desse modo, o volume é dado por V = 22.√3/4 . 20
= 4 . 1,7 . 20 /4 = 34 cm3.
Questão 30)
Em Geometria, cônicas são as curvas geradas
na intersecção de um plano que atravessa um cone. Numa superfície
cônica existem três tipos de cortes que podem ser obtidos por esse
processo e que resultam na: Parábola – O plano corta apenas uma das
folhas do cone e a secção é paralela à uma só geratriz; Elipse – O
plano corta apenas uma das folhas do cone, não passa pelo vértice e não é
paralelo a nenhuma geratriz. Caso a secção seja paralela à base, a
elipse é uma circunferência; Hipérbole – O plano corta as duas folhas do
cone. Agora, observe as quatro figuras seguintes.
As
secções corretas, de (1) a (4), são
a)
elipse, parábola, circunferência e hipérbole.
b) circunferência,
hipérbole , elipse e parábola.
c) hipérbole,
circunferência, elipse e parábola.
d) circunferência,
elipse, parábola e hipérbole.
e) parábola,
circunferência, hipérbole e elipse.
Resolução
Alternativa correta: D
De acordo com o exposto
no texto-base, a sequência correta de (1) a (4) é: circunferência, elipse,
parábola e hipérbole.