1.Uma empresa, em
processo de restauração, propôs a seus funcionários uma indenização financeira
para os que pedissem demissão, que variava em função do número de anos trabalhados.
A tabela abaixo era utilizada para calcular o valor (i) da indenização, em função
do tempo trabalhado (t).
Tempo de trabalho
(em anos) Valor da indenização
1
450
2
950
3
1450
4 1950
Baseado
na tabela acima, podemos afirmar que um funcionário com 15 anos de trabalho nessa empresa receberia uma indenização em reais de:
(A) 6.950
(B) 7.100
(C) 7.450
(D) 8.100
(E) 8.900
Vejamos :
Como a indenização aumenta de ano para ano em R$ 500,00, podemos então perceber que a relação entre (i) e (t) é do primeiro grau, ou seja do tipo i = at + b.
Vamos admitir que o ano 1 é o tempo zero, que o ano 2 é o tempo 1, e assim sucessivamente.
Então para (0, 450) → 450 = a.0 + b → b = 450 e para (1, 950) → 950 = a.1 + 450 → a = 500.
Portanto a relação em questão é i = 500t + 450, para t = 0, 1, 2 3, ...
Finalmente o funcionário com 15 anos de trabalho (t = 14) receberá uma indenização de i = 500.14 + 450 → R$ 7450,00
2. Na figura abaixo temos a imagem de uma bicicleta para adulto aro 26, em que o número 26 é o diâmetro em polegadas da roda (aro + pneu), que convertendo para centímetros é aproximadamente 66 cm.
Assim, usando uma escala em centímetros e
posicionando a bicicleta num sistema de
coordenadas como mostrado na figura acima,
aonde os eixos tangenciam a roda
dianteira, podemos afirmar que a equação dessa roda é:
(A)
x2 + y2 - 33x – 33y =
1089
(B)
x2 + y2 - 66x – 66y =
1089
(C)
x2
+ y2 - 66x – 66y = - 1089
(D)
x2 + y2 + 33x + 33y =
1089
(E)
x2 + y2+ 66x + 66y = -
1089
Vejamos :
Como a roda dianteira tangencia os eixos coordenados, então o centro da circunferência é C(33,33) e o raio é 33 cm.
Como a equação da circunferência é dada por (x - a)2 + (y - b)2 = r2, onde a e b são as coordenadas do centro e r o seu raio, entao :
(x - 33)2 + (y - 33)2 = (33)2 → x2
– 66x + 1089 + y2 – 66y + 1089 = 1089
x2 + y2 – 66x – 66y = - 1089
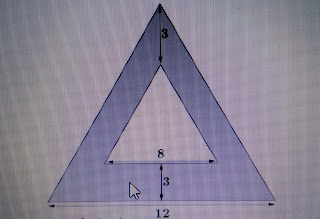
3.
Na figura abaixo
temos a representação de uma praça
triangular.
A região sombreada
representa a porção dessa praça que será destinada a prática de atividades físicas, e a parte interna (em branco) representa a porção onde serão
instalados quiosques, bancos e plantas ornamentais. As medidas destacadas na figura estão em decâmetros (dam). A área
total da região sombreada éde 52 dam2.
Podemos
assegurar que a área da região interna
é em m2:
(A)
3000 m2
(B) 3200 m2
(C)
3400 m2
(D)
3600 m2
(E)
3800 m2
Vejamos :
A área sombreada poderá ser obtida através da diferença entre as áreas dos dois triângulos, ou seja :
Área sombreada = Área Δmaior - Área Δmenor → 52 = 12.(h + 6)/2 – 8.h/2
52 = 6.(h + 6) – 4.h →
52 = 6h + 36 – 4.h → 16 = 2h → h = 8 dam
Finalmente, Área Δmenor = 8h/2 = 4h = 32 dam2 = 3200 m2
4. O rendimento de um automóvel é de 8,1 km por litro de combustível, quando trafega dentro de Fortaleza, e é de 13 quilômetros por litro de combustível, quando trafega por uma rodovia como a BR 116. Se
foram consumidos 17 litros de combustível trafegando um total de 176,9 km em Fortaleza e na BR
116, então podemos afirma que o número de
litros consumidos ao trafegar na
BR 116 foi igual a:
(A) 6,5
(B) 7,0
(C) 7,5
(D) 8,0
(E) 8,5
Vejamos :
O rendimento ´8,1 km/litro dentro da cidade e 13 km/litro na estrada.
Se foram consumidos 17 litros de combustível (x na cidade e y na estrada) trafegando um total de 176,9 km (8,1x dentro da cidade e 13y na estrada), então x + y = 17 e 8,1x + 13y = 176,9
Resolvendo o sistema, x = 17 - y e 81x + 130y = 1769 →
81(17 - y) + 130y = 1769 →1377 – 81y + 130y = 1769 →
– 81y + 130y = 1769 – 1377 →
49y = 392 → y = 8 litros
5. A Agência Nacional
de Vigilância Sanitária (Anvisa)
estabelece que os fabricantes de bebidas só podem chamar de suco
integral produtos que tiverem 100% de polpa de
fruta, de suco os produtos que
tiverem no mínimo 50% de polpa, de néctar os que tiverem de 30% a 50% de polpa, e refresco, os que tiverem menos
de 10% de polpa de frutas. Num período de dois dias, três
amigos, Ana, Beto e
Carlos, ingeriram as bebidas acima e refrigerante. Ana ingeriu 2 litros
de um refrigerante que continha 5% de
polpa de laranja e 200 ml de suco contendo 50% de polpa de abacaxi. Beto ingeriu 600 ml de néctar contendo 35% de polpa de pêssego
e 200 ml de suco contendo 50%
polpa de caju. Carlos, por sua vez, ingeriu 800 ml de refresco contendo 8% de polpa de
graviola e 200 ml de suco integral de uva. É correto afirmar
que, nesse período,
(A) Ana ingeriu 50% mais polpa que Carlos.
(B) Carlos ingeriu 20% mais polpa que Beto.
(C) Ana ingeriu 30% mais polpa que Carlos. (D) Carlos ingeriu 32% mais
polpa que Ana.
(E) Beto ingeriu 46% mais polpa que Carlos.
Vejamos :
suco integral → 100% de polpa
suco → 50% de
polpa
néctar → entre
30% a 50% de polpa
refresco → menos
de 10% de polpa
Ana → ingeriu 2 litros de um refrigerante que continha 5% de polpa de laranja e 200 ml de suco contendo 50% de polpa de abacaxi → 5% de 2000ml + 50% de 200ml = 100ml+100ml = 200ml
Beto → ingeriu 600 ml de néctar contendo 35% de polpa de pêssego e 200 ml de suco contendo 50% polpa de caju →
35% de
600ml + 50% de 200ml = 210ml + 100ml = 310ml
Carlos → ingeriu 800 ml de refresco contendo 8% de polpa de graviola e 200 ml de suco integral de uva → 8% de 800ml + 100% de 200ml = 64ml + 200ml = 264ml
Finalmente, Carlos ingeriu 32% mais polpa que Ana → 264/200 =
1,32 → 32% (letra D)
6. Cerca
de 71% da superfície da terra é coberta por água, sendo que 96,5%
dessa água encontram-se nos oceanos. Segundo o Instituto
de Pesquisa Geológica dos EUA (USGS, na
sigla em inglês), o volume de água doce
líquida do planeta nas águas subterrâneas,
em pântanos, rios e lagos é de 10.633.450 Km3. O Brasil detém em seu território 13,7 % de toda a água doce do planeta
e desse total 80% está na Amazônia. A
quantidade de água doce líquida na
Amazônia é, em m3, aproximadamente igual a
:
(A) 1,165 x 1015 m3
(B) 1,165 x 10-15
m3
(C) 1,165 x 109 m3
(D) 1,165 x 106 m3
(E) 1,165 x 10-9
m3
Vejamos :
A quantidade de água doce líquida na Amazônia →
80% de 13,7% de 10.633.450
Km3 = 0,8x0,137x10633450.109m3
1165426,12 . 109 m3
= 1,16542612 . 1015 m3
7. Na
figura abaixo temos os dados da taxa de
desocupação da população do Ceará do 2º trimestre de 2013 ao 2º trimestre de 2016, segundo dados da Pnad Contínua,
divulgados pelo Instituto Brasileiro
de Geografia e Estatística (IBGE) em
agosto de 2016.
Naquele momento, a estimativa era
de que haviam 448 mil pessoas desocupadas, o que significa
um aumento de 35,1% em relação ao mesmo período do ano anterior. Com relação
ao trimestre anterior, o aumento foi de
45 mil pessoas. Diante desses dados, podemos dizer que o aumento na quantidade de
pessoas sem ocupação em relação ao mesmo período do ano anterior e a taxa de variação em relação ao trimestre anterior são, aproximadamente,
(A) 115 mil
pessoas e 18%, respectivamente.
(B) 117 mil pessoas e 11%, respectivamente.
(C) 119 mil
pessoas e 14%, respectivamente.
(D) 120 mil
pessoas e 13%, respectivamente.
(E) 120 mil
pessoas e 15%, respectivamente.
Vejamos :
Em 2015 = x
Em 2016 → x + 35,1% de x = 448 mil → x = 331606
Portanto a variação de 2015 a 2016 = 448000 – 331606 = 116394
A taxa de variação em relação ao trimestre anterior é :
45000/(448000 – 45000)/
= 0,1116 = 11%
8. O trecho do mapa de uma cidade apresenta os quarteirões I e II. Os lados que dão para a rua A medem, respectivamente,
250 m e 200 m, e o lado do quarteirão I
voltado para a rua B mede 40 m a mais do que o do quarteirão II para a
mesma rua. Como mostra a figura abaixo.
A medida, em metros, do lado do maior dos dois quarteirões para a rua B
é:
(A) 150
(B) 170
(C) 200
(D) 250
(E) 270
Vejamos :
Através de uma proporção, vem 250/(x +40) = 200/x
250x = 200x + 8000 → 250x – 200x = 8000 → 50x = 8000
x = 160.
Portanto do lado do maior dos dois quarteirões para a rua B é (x + 40) = 200 m
Portanto do lado do maior dos dois quarteirões para a rua B é (x + 40) = 200 m
9. Um professor de arquitetura da Universidade de Fortaleza foi convidado por um prefeito de uma cidade do interior cearense a projetar uma nova escola infantil para seu município. Ao
projetar, o arquiteto utilizou 45% da
área total do terreno para o prédio que continha
as salas de aula e 15% param as salas de projeção, biblioteca e laboratório. Mesmo assim, ainda sobrou uma área
de 900 m2 para ambientes de lazer. Logo, podemos concluir que o terreno
tinha um total, em m2 de:
(A) 2250
(B) 2450
(C) 2750
(D) 3000
(E) 3250
Vejamos :
Ao projetar, o arquiteto utilizou 45% da área total para as salas de aula e 15% param as salas de projeção, biblioteca e laboratório e 900 m2 para ambientes de lazer →
45% de x + 15% de x + 900 = 100% de x → 60%x + 900 = 100% x→ 40%x = 900 → 0,4x = 900 → x = 900/0,4 → x = 2250 m2
10. O número mensal de passagens
de uma determinada empresa aérea
aumentou no ano passado nas seguintes condições: em janeiro foram vendidas 33.000 passagens; em fevereiro, 34.500; em março, 36.000. Esse padrão de crescimento se mantém para os meses subsequentes. Quantas passagens foram vendidas por essa empresa em julho
do ano passado?
(A) 42.000
(B) 42.500
(C) 43.000
(D) 43.500
(E) 44.500
Vejamos :
Em janeiro foram vendidas 33.000 passagens; em fevereiro, 34.500; em março, 36.000.
Como o padrão e crescimento foi mantido então temos uma PA de razão 1500.
Julho será seu sétimo termo → an = a1 + (n - 1).r →
a7 = 33000 +
(7 - 1).1500 → a7 = 33000 + 9000 → a7 = 42000
11. A forma de um tumor cancerígeno é aproximadamente esférico, portanto seu volume é dado, aproximadamente, pela fórmula V = 4/3. π. R3
em que r é o raio do tumor em centímetros. No exame de um paciente foi descoberto
um tumor cancerígeno de 0,73 cm de raio. Depois que o paciente foi tratado com quimioterapia,
o raio do tumor diminuiu 20%. Com base nesses dados, podemos concluir que a redução percentual
de volume do tumor do paciente foi de:
(A) 28,6%
(B) 34,2%
(C) 36,4%
(D) 44,3%
(E) 48,8%
Vejamos :
Volume antes = 4/3. π. (RA)3 = 4/3. π. 0,733
Volume depois = 4/3. π. (RD)3 = 4/3. π. (0,73 – 20% de 0,73)3 = 4/3. π.(0,8.0,73)3
V depois / V antes = 4/3. π.(0,8.0,73)3/4/3. π. 0,733 = (0,8.0,73)3/0,733 = 0,83 = 0,512 .
Portanto a redução foi de 1 – 0,512 = 0,488 = 48,8%
12. A Universidade de
Fortaleza realiza, de 17 a 21 de outubro, mais uma
edição dos Encontros Científicos. Realizado anualmente, o evento reúne o XXII Encontro de
Iniciação à Pesquisa, o XVI Encontro
de Pós Graduação e Pesquisa, o
XVI Encontro de Iniciação à
Docência, o VIII Encontro de Práticas
Docentes e o IV Encontro de Iniciação Científica
Júnior. Os Encontros Científicos da Unifor
funcionam como espaço de destaque para refletir o conhecimento científico produzido
pela Universidade e o incentivo à formação de pesquisadores. Em cinco dias, trabalhos de todo o país são apresentados nas formas oral e painel, numa troca
intensa entre professores, alunos, pesquisadores da Unifor e
visitantes de outras Instituições de
Ensino Superior (IES) e escolas de Ensino Médio.
Suponhamos que num dos dias do Encontro Científico uma quantidade x de professores da Universidade de Fortaleza se distribuem em 8 bancas examinadoras de
modo que cada professor participa
de exatamente duas bancas e cada duas bancas
têm exatamente um professor em comum. Com base nessas informações, a
quantidade de professores é:
(A) 20
(B) 23
(C) 26
(D) 28
(E) 30
Vejamos:
Para entender com relativa facilidade o
enunciado do problema, vamos evoluir a situação gradativamente.
Suponha os Professores A, B, C, D, E, ... , portanto :
ABC ABCDE
A
B C D E F G
ADE AFGHI A
H I J K L M
BDF BFJKL B H N O P Q R
CEF →4B e 6P CGJMN
C I N S
T U V
DHKMO D J O S W X Y
E I
LNO →6B e 15P E K P T W Z α
F L Q U
X Z β
G M R V Y α β → 8B e
28P
13. Um hospital particular possui 42 médicos, e sabe-se que cada médico
tem pelo menos uma das especializações entre Cardiologia e
Gastrenterologia. Além disso, 20% dos
que tem especialização em Cardiologia também tem especialização em Gastrenterologia e 80% dos que tem especialização em Gastrenterologia também tem especialização em Cardiologia. O número
de médicos que tem as duas especializações é:
(A) 8
(B) 10
(C) 14
(D) 17
(E) 20
Vejamos :
20% dos que tem especialização
em Cardiologia também tem em Gastrenterologia → y = 20% (x
+ y) → y = 0,2x + 0,2y → 0,8y = 0,2x →
8y = 2x → 4y = x.
80% dos que tem especialização em Gastrenterologia também tem em Cardiologia → y = 80%(z + y) → y = 0,8z + 0,8y→ 0,2y = 0,8z →
2y = 8z → y = 4z → z = y/4
Cardiologia ou Gastrenterologia → x + y + z = 42 médicos →
4y + y + y/4 = 42 → 16y + 4y + y = 168 → 21y = 168 → y = 8
14. A Universidade de Fortaleza conta com um Programa de Monitoria Institucional e Voluntária
cuja finalidade é favorecer a participação dos alunos na execução de projetos de
ensino e na vida acadêmica
universitária, além de incentivar a melhoria no processo
ensino/aprendizagem, fortalecendo a relação aluno/professor.
No final do primeiro semestre do ano 2016 na Universidade de Fortaleza, 40 alunos participaram de uma pesquisa que objetivou analisar a frequência com que estes utilizaram o atendimento extraclasse do professor e/ou do monitor de uma determinada disciplina. Obteve-se o seguinte
resultado: 20% dos alunos procuraram atendimento tanto do professor quanto do monitor; 30% dos alunos procuraram somente o atendimento do monitor: 15% dos alunos não opinaram e
4 alunos não procuraram atendimento do professor nem do monitor. Considerando
que os alunos que não opinaram
não procuraram atendimento, o
número de alunos que procurou atendimento somente
do professor é igual a:
(A) 8
(B) 10
(C) 18
(D) 20
(E) 24
Vejamos :
Universo = 40 alunos (U)
Monitor e Professor = 20% de 40 = 8 alunos (M∩P)
Somente o Monitor = 30% de 40 = 12 alunos (M - P)
Não opinaram = 15% de 40 = 6 alunos → U - (M U P)
Não procuram atendimento = 4 alunos → U - (M U P)
Como M U P = (M - P) + (M ∩ P) + (P - M), então
40 – 6 – 4 = 12 + 8
+ (P - M) → 30 = 20 + (P - M)
Somente o Monitor (P - M) = 10
15. A Universidade de Fortaleza possui quatro gráficas que atendem
a todo seu corpo docente e discente
desde as impressões simples as mais aprimoradas. Suponhamos que uma das gráficas possui 8 copiadoras igualmente produtivas,
que trabalhando 4 horas por dia, produzem em 5 dias 160.000 cópias. Quantos dias de
trabalho serão necessários para que 7dessas
copiadoras, trabalhando 6 horas por dia,
produzam 210.000 cópias?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Vejamos :
A situação apresentava caracteriza um regra de três composta.
↑ 8 copiadoras ↑ 4h/dia ↓ 5 dias ↓160000 cópias
7 copiadoras 6h/dia
x dias 210000 cópias
Inversa inversa direta
5/x = 7/8 . 6/4 . 160000/210000 → 5/x = 7/8 . 6/4 . 16/21
5/x = 7.6.16/8.4.21→ 5/x = 6.2/4.3→ 5/x = 1→
x = 5 dias