QUESTOES VESTIBULAR UNICAMP 2016 - TIPO ANALITICA- COMENTADAS

1. (Unicamp 2016)  Considere o triângulo exibido na figura abaixo, com lados de comprimentos a, b e c  e ângulos α, β e γ.

                                

a) Suponha que a sequência (α, β, γ) é uma progressão aritmética (PA). Determine a medida do ângulo β.

b) Suponha que a sequência (a, b, c) é uma progressão geométrica (PG) de razão q = √2. Determine o valor de tan β

  

Resposta da questão 1:
 a) Se (α, β, γ) é uma PA, então a soma de seus termos será 180, pois a soma dos ângulos internos de um triângulo é sempre 180⁰. Assim, pode-se escrever:

    PA → (α, β, γ) = (β - r, β, β + r) → S = 180 = (β – r + β + r).3/2 → β = 60⁰

  

     b) Se (a, b, c) é uma PG de raiz q = √2, então pode-se escrever:

 PG → (a, b, c) = (a, a√2, 2a)

Pela lei dos cossenos, tem-se:

(a√2)² = a² + (2a)² – 2 . a . 2a . cosβ → 5a² – 4a².cosβ → cosβ = 3/4

    Pela relação fundamental:

   Sen² β + cos²β = 1 → sen²β = 7/16 → senβ = √7/4

   Por fim, calculando a tangente: tgβ = senβ/cosβ = (√7/4)/(3/4)→tgβ = √7/3

   

  

2. (Unicamp 2016)  Considere a função f(x) = |2x - 4| + x – 5, definida para todo número real x.

a) Esboce o gráfico de y = f(x) no plano cartesiano para -4 ≤ x ≤ 4.

 

 b) Determine os valores dos números reais a  e b para os quais a equação log_a^{(x + b)} = f(x), admite como soluções x₁ = -1 e x₂ = 6.

  

  Resposta da questão 2:
 a) Fazendo os cálculos, tem-se: f(x) = |2x - 4| + x – 5

     f(-4) = |-8 - 4| - 4 – 5 = 3 → (- 4, 3)

     f(-1) = |-2 - 4| - 2 – 5 = 0 → (- 1, 0)

     f(0) = |0 - 4| + 0 – 5 = - 1 → (0, -1)

     f(2) = |4 - 4| + 2 – 5 = - 3 → (4, -3)

     f(3) = |6 - 4| + 3 – 5 = - 3 → (3, -3)

     f(4) = |8 - 4| + 4 – 5 = 3 → (4, 3)

                           Montando o gráfico:

b) Substituindo uma das raízes dadas e desenvolvendo a equação:

    log_a^{(x + b)} = f(x) → log_a^{(x + b)} = |2x - 4| + x – 5

    log_a^{(-1 + b)} = |2(-1) - 4| + (-1) – 5 → log_a^{(-1 + b)} = 0 → a⁰ = -1 + b → b = 2

Substituindo a segunda raiz dada e desenvolvendo a equação:

    log_a^{(6+ 2)} = |2.6 - 4| + 6 – 5 → log_a⁸ = 9 → a⁹ = 8 → a = ⁹√8 → a = ³√2

Assim, os valores dos números reais a  e b  são ³√2 e 2, respectivamente.  

3. (Unicamp 2016)  Considere o polinômio cúbico p(x) = x³ – 3x + a, onde a  é um número real.

a)    No caso em que p(1), determine os valores de x para os quais a matriz A abaixo não é invertível.

b) Seja b um número real não nulo e i a unidade imaginária, isto é, i² = -1. Se o número complexo z = 2 + bi  é uma raiz de p(x), determine o valor de |z|.

  

Resposta da questão 3:
 a) Se p(1) = 0, pode-se escrever: p(1) = 1 – 3 + a = 0 → a = 2

Para que a matriz A não seja invertível, seu determinante deve ser igual a zero. Assim, pode-se escrever:

b) Supondo como raízes do polinômio os números {2 + bi, 2 – bi, r} pode-se escrever: 2 + bi + 2 – bi + r = 0 → r = -4

Supondo - 4  raiz, pode-se deduzir o valor de a : -64+12+a = 0 → a = 52

Fazendo o produto das três raízes (Relações de Girard), pode-se escrever: (2 + bi).(2 – bi).(- 4) = - 52 → 4 + b² = 13

Assim, |z| será: |2 + bi| = √(4 + b²) → |z| = √13

4. (Unicamp 2016)  Considere os três sólidos exibidos na figura abaixo, um cubo e dois paralelepípedos retângulos, em que os comprimentos das arestas, a e b,  são tais que a > b > 0.

a) Determine a razão r = a/b para a qual o volume de S₁ é igual à soma dos volumes de S₂ e S₃

b) Sabendo que a soma dos comprimentos de todas as arestas dos três sólidos é igual a 60cm, determine a soma das áreas de superfície dos três sólidos. 

Resposta da questão 4:
 a) Com os dados do enunciado pode-se escrever:

    S₁ = S₂ + S₃ → a³ = a².b + a.b²

    Desenvolvendo esta equação, tem-se:

   a³ - a².b - a.b² = 0 → a(a² - a.b + b²) = 0 → a² - a.b + b² = 0

   a²/b² - a.b/b² + b²/b² = 0 → (a/b)² - a/b – b²/b² = 0 → (a/b)² - a/b – 1 = 0

   r² – r – 1 = 0 → ∆ = 1 – 4 . 1 . (-1) → ∆ = 5 → r = (1 + √5) /2

b) Sendo a soma das medidas de todas as arestas dos três sólidos igual a

   60, pode-se escrever: 12a + 8a + 4b + 8b + 4a = 60 → 2a + b = 5 

A soma das áreas dos três sólidos pode ser escrita como:

A_T = 6a² + 2a² + 4ab + 2b² + 4ab = 8a² + 8ab + 2b² = 2.( 4a² + 4ab + b²)

A_T = 2.(2a + b)² → Como 2a + b = 5, A_T = 2.5² → A_T = 50 cm²

  

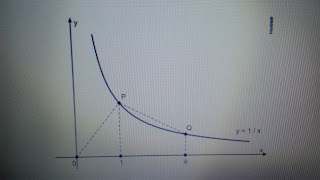
5. (Unicamp 2016)  A figura abaixo exibe o gráfico da função f(x) = 1/x, definida para todo número real x > 0. Os pontos P e Q  têm abscissas

x = 1 e x = a, respectivamente, onde a é um número real e a > 1.

a) Considere o quadrilátero T com vértices em (0,0), P, Q e (a, 0). Para a = 2, verifique que a área de T é igual ao quadrado da distância de P a Q .

b) Seja r a reta que passa pela origem e é ortogonal à reta que passa por P e Q. Determine o valor de a para o qual o ponto de intersecção da reta r com o gráfico da função f tem ordenada y = a/2.

  

  Resposta da questão 5:
 a) Se a abscissa do ponto P é igual a 1, então pela função f(x) dada, P terá coordenadas (1, 1). Analogamente, se a = 2, então pela função f(x) dada, Q  terá coordenadas (2, 1/2). Assim, a área do quadrilátero T será:

   S_T = 1.1/2 + (1.1/2)/2 + 1.1/2 = 1 + 1/4 →S_T = 5/4

Calculando o quadrado da distância entre P e Q tem-se:

d_PQ = √[(1 - 2)² + (1 - 1/2)²] = √(1 = 1/4) = √5/4

b) Seja I o ponto de intersecção entre a reta r e a função f(x). Se sua coordenada y é igual a a/2, então, pela função f(x) sua coordenada x  será 2/a. Ou seja, o ponto i  tem coordenadas (2/a, a/2).

Considerando como s a reta que passa por P e Q, tem-se que as coordenadas do ponto P são (1, 1), e do ponto Q são (a, 1/a). O coeficiente angular desta reta será: a_s = (1/a - 1) / (a - 1) = - 1/a

    Logo, o coeficiente angular da reta r  que passa pela origem e é      ortogonal à reta que contém P e Q será igual a α_r = a (condição de perpendicularidade).

Assim, a equação da reta  pode ser escrita como:

Y – 0 = a. (x - 0) → y = ax

   Como o ponto I pertence à reta r e tem suas coordenadas (2/a, a/2), pode-se escrever: y = ax → a/2 = a. 2/a → a = 4

  

6. (Unicamp 2016)  O gráfico de barras abaixo exibe a distribuição da idade de um grupo de pessoas.

a) Mostre que, nesse grupo, a média de idade dos homens é igual à média de idade das mulheres.

b) Escolhendo ao acaso um homem e uma mulher desse grupo, determine a probabilidade de que a soma de suas idades seja igual a 49 anos.

Resposta da questão 6:
 a) Pelo gráfico, pode-se calcular a média de homens e mulheres:

M_homens = (4.21+5.22+4.23+1.24+2.25)/(4+5+4+1+2)=360/16= 22,5 anos

M_mulheres = (5.21+2.22+3.23+3.24+1.25)/(5+2+3+3+1)=315/14= 22,5 anos

b) Pelo gráfico, sabe-se que o grupo possui 14 mulheres e 16 homens. Dadas as possibilidades de idade, a soma de idades de um homem e uma mulher escolhidos ao acaso será 49 somente se eles tiverem 24 e 25 anos.

Assim, há de se considerar dois cenários:

- Mulher com 25 anos e homem com 24 anos

P(M25) = 1/14 ; P(H24) = 1/16 → P(C1) = 1/14 . 1/16 = 1/ 224

- Homem com 25 anos e mulher com 24 anos

P(M24) = 3/14 ; P(H25) = 2/16 → P(C1) = 3/14 . 2/16 = 6/ 224

 Logo, escolhendo ao acaso um homem e uma mulher desse grupo, a    probabilidade de que a soma de suas idades seja igual a 49 anos será:

P(total) = 1/224 + 6/224 → P(total) = 7/224 = 1/32

   

QUESTOES VESTIBULAR UNICAMP 2016 - COMENTADAS

1. (Unicamp 2016)  Seja (a, b, c) uma progressão geométrica de números reais com a ≠ 0. Definindo s = a + b + c, o menor valor possível para s/a é igual a :

a) 1/2   

b) 2/3   

c) 3/4   

d) 4/5   

  

Resposta da questão 1:[C]

Tem-se que (a, b, c) = (a, aq, aq²), com a ≠ 0 e q sendo a razão da

progressão geométrica. Desse modo, vem :

s/a = (a + aq + aq²) / a = q² + q + 1 = (q + 1/2)² + 3/4

Portanto, o valor mínimo de s/a é 3/4, ocorrendo para q = - 1/2  

2. (Unicamp 2016)  O gráfico abaixo exibe o lucro líquido (em milhares de reais) de três pequenas empresas A, B e C, nos anos de 2013 e 2014.

   

Com relação ao lucro líquido, podemos afirmar que

a) A teve um crescimento maior do que C.   

b) C teve um crescimento maior do que B.   

c) B teve um crescimento igual a A.   

d) C teve um crescimento menor do que B.   

Resposta da questão 2:[B]

É fácil ver que A teve um decrescimento, enquanto que B e C tiveram um crescimento. Além disso, o crescimento de B foi de 100 milhares de reais e o crescimento de C foi de 200 milhares de reais. Portanto, C teve um crescimento maior do que o de .  

  

3. (Unicamp 2016)  Considere a função afim f(x) = ax + b definida para todo número real x, onde a e b são números reais. Sabendo que f(4) = 2, podemos afirmar que f(f(3)) + f(5) é igual a :

a) 5   

b) 4   

c) 3   

d) 2   

  

Resposta da questão 3:[D]

Tem-se que f(4) = 2 → 4a + b = 2. Além disso, como f(3) = 3a + b e

f(5) = 5a + b, vem f(3) + f(5) = 3a + b + 5a+ b = 8a + 2b = 2(4a + b) = 4

Portanto, segue que f(f(3)) + f(5) = f(4) + 2.  

4. (Unicamp 2016)  Considere o gráfico da função y = f(x) exibido na figura a seguir.

                             

O gráfico da função inversa y = f^-1(x) é dado por :

     

Resposta da questão 4: [C]

Lembrando que o gráfico de uma função e o de sua inversa são simétricos em relação à reta y = x segue-se que o gráfico de y = f^-1(x) é o da alternativa [C].  

5. (Unicamp 2016)  Em uma matriz, chamam-se elementos internos aqueles que não pertencem à primeira nem à última linha ou coluna. O número de elementos internos em uma matriz com 5 linhas e 6 colunas é igual a :

a) 12   

b) 15   

c) 16   

d) 20   

  

  Resposta da questão 5: [A]

O resultado pedido é igual a (5 - 2).(6 - 2) = 12.  

6. (Unicamp 2016)  Considere o sistema linear nas variáveis reais x, y, z  e w, tal que x – y = 1 ; y + z = 2 ; w – z = 3.

Logo, a soma x + y + z + w é igual a :

a) -2   

b) 0   

c) 6   

d) 8   

Resposta da questão 6:[D]

Somando todas as equações do sistema, vem x + w = 6. Logo, somando essa equação à segunda, obtemos x + y + z + w = 6 + 2 = 8  

  

7. (Unicamp 2016)  Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a :

a) 1/4   

b) 3/8   

c) 1/2   

d) 3/4   

  

Resposta da questão 7: [C]

Existem P₄³ = 4!/3! modos de obter exatamente 3 três caras em 4 lançamentos. Por outro lado, existem apenas duas maneiras de obter 3 caras consecutivamente: ccck e kccc. Em consequência, a probabilidade pedida é 2/4 ou seja, 1/2.  

8. (Unicamp 2016)  Um cilindro circular reto, cuja altura é igual ao diâmetro da base, está inscrito numa esfera. A razão entre os volumes da esfera e do cilindro é igual a :

a) 4√2/3   

b) 4/3   

c) 3√2/4   

d)√2   

  

  Resposta da questão 8:[A]

Sejam r e R, respectivamente, o raio da esfera e o raio do cilindro.

Sabendo que a relação entre o raio da esfera circunscrita ao cilindro equilátero e o raio do cilindro é r = R√2, temos :

(4πr³/3) / (2πR³) = 2/3 . (r/R)³ = 2/3 . (√2)³ = 4√2/3

9. (Unicamp 2016)  Considere o círculo de equação cartesiana x² + y² = ax + by, onde a e b são números reais não nulos. O número de pontos em que esse círculo intercepta os eixos coordenados é igual a :

a) 1   

b) 2   

c) 3   

d) 4   

  

Resposta da questão 9: [C]

É fácil ver que a circunferência x² + y² = ax + by intersecta a origem dos eixos cartesianos. Ademais, tomando x = 0, obtemos y = 0 ou y = b. Por outro lado, fazendo y = 0, encontramos x = 0 ou x = a.  Em consequência, podemos afirmar que a resposta é 3.  

10. (Unicamp 2016)  A solução da equação na variável real x,  log_x^{(x + 6)} = 2, é um número :

a) primo.   

b) par.   

c) negativo.   

d) irracional.   

  

Resposta da questão 10:[A]

Sabendo que log_a^b = c ↔ a^c = b, para quaisquer a e b reais positivos, e

a ≠ 1, temos log_x^{(x + 6)} = 2 → x² – x – 6 = 0 → x = 3, que é um número primo.  

11. (Unicamp 2016)  A figura abaixo exibe um quadrilátero ABCD, onde AB = AD e BC = CD = 2 cm.

             

A área do quadrilátero ABCD é igual a :

a) √2 cm²   

b)  2 cm²   

c)  2√2 cm²   

d) 3 cm²   

  

Resposta da questão 11:[B]

Considere a figura.

                          

Aplicando a Lei dos Cossenos no triângulo BCD, temos :

BD² = BC² + CD² – 2.BC.CD.cosBED → BD² = 2² + 2² – 2.2.2.√2/2 →

BD = 2√(2-√2) cm.

Como AC é bissetriz de BAD e BED, segue que os triângulos retângulos ABE e ADE são congruentes.

Logo, podemos concluir que AE = 2√(2-√2) cm.

A resposta é dada por ABD + BCD = 1/2 . BD . AE + 1/2 . BC . CD . senBED

= [2√(2-√2). √(2-√2)]/2 + 1/2 . 2 . 2.√2/2 = 2 - √2 + √2 = 2 cm²

  

12. (Unicamp 2016)  Considere o número complexo z = (1 + ai) / (a - i), onde a é um número real e i é a unidade imaginária, isto é, i² = -1 O valor de z²⁰¹⁶ é igual a :

a) a²⁰¹⁶   

b) 1   

c) 1 + 2016i   

d) i   

Resposta da questão 12:[B]

Tem-se que z = (1 + ai) / (a - i) = z = [(1 + ai) / (a - i)] . [ (a + i) / (a + i) =

(a + i + a²i - a) / (a² + 1) = i

Portanto, o valor de z²⁰¹⁶ é i²⁰¹⁶ = i⁰ = 1  

13. (Unicamp 2016)  Considere o polinômio cúbico p(x) = x³ + x² –ax – 3, onde a é um número real. Sabendo que r e -r são raízes reais de p(x) podemos afirmar que p(1) é igual a :

a) 3   

b) 1   

c) -2   

d) -4   

  

Resposta da questão 13:[D]

Se r e -r são raízes de p, então p(r) = p(-r) = 0. Logo, segue que

r³ + r² –ar – 3 = 0 e -r³ + r² –ar – 3 = 0. Somando essas equações, obtemos

2r² – 6 = 0, ou seja, r² = 3. 

Por outro lado, sendo α a outra raiz real de p, pelas Relações de Girard,

vem r + (-r) + α = -1/1 → α = - 1.

 Em consequência, tem-se p(x) = (x² – r²).(x - α) = (x² – 3)(x + 1) e, portanto,

podemos afirmar que p(1) é igual a p(1) = (1² – 3)(1 + 1) = -4

14. (Unicamp 2016)  Considere a matriz quadrada de ordem 3 onde x é um número real.

                           

Podemos afirmar que :

a) A não é invertível para nenhum valor de x.   

b) A é invertível para um único valor de x   

c) A é invertível para exatamente dois valores de x.   

d) a é invertível para todos os valores de .   

  

Resposta da questão 14:[D]

Calculando o determinante da matriz A, encontramos

                

Portanto, como det A ≠ 0, para todo x real, segue-se que A é invertível para todos os valores de x.