QUESTÕES VESTIBULAR FUVEST 2017 - COMENTADAS

1. (Fuvest 2017)  Considere as funções f(x) = x² + 4 e g(x) = 1 + log_1/2x , em que o domínio de f é o conjunto dos números reais e o domínio de g é o conjunto dos números reais maiores do que 0.

Seja h(x) = 3f(g(x) + 2g(f(x), em que x > 0. Então, h(2) é igual a :

a) 4   

b) 8   

c) 12   

d) 16   

e) 20   

Resposta da questão 1:[B]

f(g(2)) = f[1 + log_1/2²] = f(1 - 1) = f(0) = 4

g(f(2)) = g(2² + 4) = g(8) = 1 + log_1/2⁸ = 1 – 3 = - 2

h(2) = 3. f(g(2)) + 2. g(f(2)) = 3.4 + 2.(-2) = 8

  

  

2. (Fuvest 2017)  Cláudia, Paulo, Rodrigo e Ana brincam entre si de amigo-secreto (ou amigo-oculto). Cada nome é escrito em um pedaço de papel, que é colocado em uma urna, e cada participante retira um deles ao acaso. A probabilidade de que nenhum participante retire seu próprio nome é

a) 1/4   

b) 7/24   

c) 1/3   

d) 3/8   

e) 5/12   

Resposta da questão 2:[D]

Supondo que a sequência ACPR represente a opção na qual todos os amigos retiram o próprio nome e sabendo que o total de permutações para os quatro amigos é 24 (P₄ = 4! = 24), pode-se contar o número de permutações caóticas da sequência com a ajuda de um diagrama de árvore:

Logo, de um total de 24 permutações, em 9 delas nenhum participante retire seu próprio nome. A probabilidade será de: 9/24 = 3/8.   

  

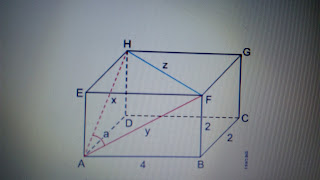
3. (Fuvest 2017)  O paralelepípedo reto-retângulo ABCDEFGH, representado na figura, tem medida dos lados AB = 4, BC = 2 e BF = 2.

 

O seno do ângulo HAF é igual a :

a) 1/2√5   

b) 1/√5   

c) 2/√10   

d) 2/√5   

e) 3/√10   

Resposta da questão 3:[E]

 

∆ABF → y² = 4² + 2² → y² = 20 → y = 2√5

∆EHF → z² = 4² + 2² → z² = 20 → z = 2√5

∆EHA → x² = 2² + 2² → x² = 8 → x = 2√2

Lei dos cossenos : z² = x² + y² – 2xycos a → 20 =8 + 20- 2.2√2.2√5.cos a

8√10.cos a = 8 → cos a = 1/√10 → sen a = 3/√10

  

4. (Fuvest 2017)  Um reservatório de água tem o formato de um cone circular reto. O diâmetro de sua base (que está apoiada sobre o chão horizontal) é igual a 8 m. Sua altura é igual a 12 m. A partir de um instante em que o reservatório está completamente vazio, inicia-se seu enchimento com água a uma vazão constante de 500 litros por minuto.

O tempo gasto para que o nível de água atinja metade da altura do reservatório é de, aproximadamente,

Dados:

- π é aproximadamente 3,14.

- O volume V do cone circular reto de altura h e raio da base r é

V = 1/3 .π.r².h.

a) 4 horas e 50 minutos.   

b) 5 horas e 20 minutos.   

c) 5 horas e 50 minutos.   

d) 6 horas e 20 minutos.   

e) 6 horas e 50 minutos.   

  

  

Resposta da questão 4:[C]

De acordo com o enunciado:

 

Considerando:

V = volume total do cone

v' = volume cheio (tronco)

v'' = volume vazio (topo'

H = 12 = altura total

H = 6 = altura topo / altura tronco

Pode-se calcular:

V/v'' = (H/h)³ → V/v'' = (12/6)³ → V/v'' = 8 → V = 8v''

v' + v' = V → v' + V/8 = V → v' = 7/8 V

V = 1/3 . π . R² . H = 1/3 . 3,14 . 4² . 12 → V = 200,96

v' = 7/8 V = 7/8 . 200,96 = 175,85 m³

Tempo : 500L / min = 0,5 m³ / min

portanto se  1 min → 0,5 m³ entao 175,85 m³ → t min

t = 175,58 / 0,5 → t = 351,7 min ≈ 5h 50 min

5. (Fuvest 2017)  Duas circunferências com raios 1 e 2 têm centros no primeiro quadrante do plano cartesiano e ambas tangenciam os dois eixos coordenados. Essas circunferências se interceptam em dois pontos distintos de coordenadas (x₁ , y₁ ) e (x₂ , y₂ ) .

O valor de (x₁ + y₁ )²  + (x₂ + y₂ )²  é igual a :

a) 5/2   

b) 7/2   

c) 9/2   

d) 11/2   

e) 13/2   

  

Resposta da questão 5:[C]

Se as circunferências tangenciam os dois eixos coordenados e estão no primeiro quadrante, então as coordenadas de seus centros são iguais ao comprimento de seu raio. Assim, pode-se escrever:

ʎ₁ → raio = 1 e centro C₁(1, 1)

ʎ₂ → raio = 2 e centro C₂(2, 2)

ʎ₁ : (x-1)² + (y-1)² = 1² → x² + y² - 2x – 2y + 1 = 0

ʎ₂ : (x-2)² + (y-2)² = 2² → x² + y² - 4x – 4y + 4 = 0

Fazendo ʎ_{1 -} ʎ₂ tem-se uma reta r que é a reta que passa pelos pontos de intersecção das circunferências. Como os pontos (x₁, y₁) e (x₂, y₂)  pertencem a essa reta, pode-se escrever:

ʎ_{1 -} ʎ₂ = r → r : 2x + 2y – 3 = 0 → x + y = 3/2

x₁ + y₁ = x₂ + y₂ = 3/2 → (x₁ + y₁)² + (x₂ + y₂)² = (3/2)² + (3/2)² = 18/4 = 9/2  

6. (Fuvest 2017)  Na figura, o retângulo ABCD tem lados de comprimento AB = 4 e BC = 2. Sejam M o ponto médio do lado BC e N o ponto médio do lado CD Os segmentos AM e AC interceptam o segmento BN nos pontos E e F, respectivamente.

 

A área do triângulo AEF é igual a :

a) 24/25   

b) 29/30   

c) 61/60   

d) 16/15   

e) 23/20   

  

Resposta da questão 6:[D]

De acordo com o enunciado:

 

∆NFC ≈ ∆AFB → 2/4 = x/y → y = 2x.

Como x + y = 2 → x + 2x = 2 → x = 2/3 e y = 4/3

∆MEN ≈ ∆MAN → 1/4 = a/b → b = 4a .

Como a + b = 1 → a + 4a = 1 → a = 1/5 e b = 4/5

Assim, a área do triângulo AEF será: S_∆ABF - S_∆ABE

S_∆AEF = 4y/2 – 4b/2 = (4.4/3)/2 - (4.4/5)/2 = 8/3 – 8 /5 = 16/15

  

7. (Fuvest 2017)  O retângulo ABCD, representado na figura, tem lados de comprimento AB = 3 e BC = 4. O ponto P pertence ao lado BC e BP = 1. Os pontos R, S e T pertencem aos lados AB, CD e AD, respectivamente. O segmento RS é paralelo a AD e intercepta DP no ponto Q. O segmento TQ é paralelo a AB.

 

Sendo x o comprimento de AR, o maior valor da soma das áreas do retângulo ARQT do triângulo CQT e do triângulo DQS para x variando no intervalo aberto ]0,3[, é :

a) 61/8   

b) 33/4   

c) 17/2   

d) 35/   

e) 73/8   

  

Resposta da questão 7:[A]

Diante do exposto, pode-se desenhar:

 

A soma das áreas hachuradas será:

S(x) = x²/2 + 3.(3-x)/2 + x.(x-4) =1/2 . (-x² + 5x + 9)

S_max = 1/2 . -(5²-4.(-1).9) /4.(-1) → S_max = 61/8

   

  

8. (Fuvest 2017)  O polinômio P(x) = x³ – 3x² + 7x - 5 possui uma raiz complexa µ cuja parte imaginária é positiva.  A parte real de µ³ é igual a :

a) -11   

b) -7   

c) 9   

d) 10   

e) 12   

  

Resposta da questão 8:[A]

O polinômio em questão possui três raízes. Se a + bi é raiz, a - bi também será. O polinômio também admite raiz 1,  pois P(1) = 1 – 3 + 7 – 5 = 0. Assim, aplicando-se Briot-Ruffini, pode-se escrever:

 

x² – 2x + 5 = 0 → x = 1 – 2i ou x = 1 + 2i.

µ = 1 + 2i → µ³ = (1 + 2i)³ = 1 + 6i – 12 – 8i → µ³ = - 11 – 2i

Assim, a parte real de µ³ é igual a -11.  

 

9. (Fuvest 2017)  Uma quantidade fixa de um gás ideal é mantida a temperatura constante, e seu volume varia com o tempo de acordo com a seguinte fórmula: V(t) = log₂[5 +2sen(πt)], 0 ≤ t ≤ 2, em que t é medido em horas e V(t) é medido em m³. A pressão máxima do gás no intervalo de tempo [0,2] ocorre no instante :

a) 0,4   

b) 0,5   

c) 1   

d) 1,5   

e) 2   

Resposta da questão 9: [D]

Pela equação de Clapeyron (da Química): PV = nRT

P = pressão

V = volume

N = quantidade de matéria (n⁰ mols)

R = costante universal dos gases

T = temperatura

Assim, percebe-se que pressão e volume são inversamente proporcionais: a pressão do gás é máxima quando o volume é mínimo. Como a função logarítmica dada é sempre crescente, o volume será mínimo quando o logaritmando for mínimo.

Ou seja: logaritimando → [5 + 2 sen(πt)]

f_min(t) = 5 + 2 sen(πt) → sen(πt) debe ser minimo

πt = 3π/2 + 2kπ → t = 3/2 + 2k → t = 3/2 = 1,5

   

  

10. (Fuvest 2017)  João tem R$150,00 para comprar canetas em 3 lojas. Na loja A, as canetas são vendidas em dúzias, cada dúzia custa R$40,00 e há apenas 2 dúzias em estoque. Na loja B, as canetas são vendidas em pares, cada par custa R$7,60 e há 10 pares em estoque. Na loja C, as canetas são vendidas avulsas, cada caneta custa R$3,20 e há 25 canetas em estoque. O maior número de canetas que João pode comprar nas lojas A, B e C utilizando no máximo R$150,00 é igual a :

a) 46   

b) 45   

c) 44   

d) 43   

e) 42   

  

Resposta da questão 10:[B]

A primeira vista seria mais vantajoso comprar todas as canetas em C, pois é o local mais barato e, depois comprar o restante em A (aproximadamente 40 / 12 = R$ 3,33 / caneta ), e por último na loja C (7,60 / 2 = R$ 3,80 / caneta ). Assim, seriam compradas 25 canetas por R$3,20 cada, uma dúzia por R$40,00 e três pares canetas por R$7,60 cada, totalizando 43 canetas.

Porém, é necessário analisar outras possibilidades. É importante ressaltar que, enquanto houver pares em A ou C, é mais vantajoso comprar dessas lojas uma vez que o preço em B, é o maior praticado. Assim, se comprarmos duas dúzias em A (evitando comprar canetas em B), seriam gastos R$80,00 e, com o valor restante de R$70,00 seria possível comprar mais 21 canetas avulsas, totalizando 45 canetas. Esse será o maior número de canetas que João irá comprar (todas as outras possibilidades envolvem comprar mais canetas em B, que é o local com maior preço, resultando em menores quantidades).  

11. (Fuvest 2017)  Sejam a e b dois números inteiros positivos. Diz-se que a e b são equivalentes se a soma dos divisores positivos de a coincide com a soma dos divisores positivos de b. Constituem dois inteiros positivos equivalentes:  

a) 8 e 9   

b) 9 e 11   

c) 10 e 12   

d) 15 e 20   

e) 16 e 25   

Resposta da questão 11:[E]

Calculando os divisores:

Divisores de 8 → {1, 2, 4, 8} → Soma = 15

Divisores de 9 → {1, 3, 9} → Soma = 13

Divisores de 10 → {1, 2, 5, 10} → Soma = 18

Divisores de 11 → {1, 11} → Soma = 12

Divisores de 12 → {1, 2, 3 4, 6, 12} → Soma = 28

Divisores de 15 → {1, 3, 5, 15} → Soma = 24

Divisores de 16 → {1, 2, 4, 8, 16} → Soma = 31

Divisores de 25 → {1, 5, 25} → Soma = 31

Logo, 16 e 25 são dois inteiros positivos equivalentes.