1. (Unicamp 2017) Sabe-se que, em um grupo de 10 pessoas, o livro A foi lido por 5 pessoas
e o livro B foi lido por 4 pessoas. Podemos afirmar corretamente que, nesse
grupo,
a) pelo menos uma pessoa leu os dois
livros.
b) nenhuma pessoa leu os dois livros.
c) pelo menos uma pessoa não leu nenhum
dos dois livros.
d) todas as pessoas leram pelo menos um
dos dois livros.
Resposta da questão 1:[C]
A única
alternativa correta é a [C]. Se cinco pessoas leram o livro A e quatro pessoas
distintas leram o livro B, há um total de 9 pessoas, sendo possível que ao
menos uma pessoa não tenha lido nenhum dos livros.
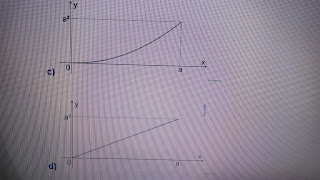
2. (Unicamp 2017) Considere o quadrado de lado a > 0 exibido na figura abaixo. Seja A(x)
a função que associa a cada 0 ≤ x ≤ a, a área da região indicada pela cor
cinza.
O gráfico da função y = A(x) no plano cartesiano é dado por
Resposta da questão 2:[D]
Calculando: A(x)
= a2 - [ 2. a.(a-x)/2] = a2 – a2 + ax → A(x) =
ax
O único gráfico
que apresenta uma função linear é o mostrado na alternativa [D].
3. (Unicamp 2017) Seja f(x) uma função tal que para todo número real x temos que xf(x-1) =
(x-3)f(x) + 3. Então, f(1) é igual a :
a) 0
b) 1
c) 2
d) 3
Resposta da questão 3:[B]
Calculando : x = 0 → 0f(0-1) = (0-3)f(0) + 3 → f(0) = 1
x = 1 → 1f(1-1) =
(1-3)f(1) + 3 → f(0) = -2f(1) + 3 → f(1) = 1
4. (Unicamp 2017) Considere as funções f(x) = 3x e g(x) = x3, definidas para todo
número real x. O número de soluções da equação f(g(x))=g(f(x)) é igual a :
a) 1
b) 2
c) 3
d) 4
Resposta da questão 4:[C]
Calculando: f(g(x)) = f(x3) e
g(f(x)) = g(3x) , vem : x3 = 3x → x3 - 3x = 0
x . (x2 – 3 ) = 0 → xʹ = 0,
xʹʹ = √3 e xʹʹʹ = - √3
5. (Unicamp 2017) Sendo a um número real, considere a matriz A(2x2) tal que a11 =
1, a12 = a, a21 = 0 e a22 = -1. Então, A2017
é igual a :
Resposta da questão 5:[B]
Calculando:
6. (Unicamp 2017) Sejam a e b números reais. Considere, então, os dois sistemas lineares abaixo, nas variáveis x, y e z :
x – y = a e z –
y = 1 ; x + y = 2
e y + z = b.
Sabendo que esses dois sistemas
possuem uma solução em comum, podemos afirmar corretamente que :
a) a – b = 0
b) a + b = 1
c) a – b = 2
d) a + b = 3
Resposta da questão 6:[D]
Se o sistema
possui solução em comum, o sistema formado pelas quatro equações tem solução. Portanto, pode-se escrever:
x – y = a ;
z – y = 1 ; x + y = 2 ;
y + z = b.
z – y = 1 e
x + y = 2 → z + x = 3
x – y = a e
y + z = b → z + x = a + b → a
+ b = 3
7. (Unicamp 2017) Um dado não tendencioso de seis faces será lançado duas vezes. A
probabilidade de que o maior valor obtido nos lançamentos seja menor do que 3 é
igual a :
a) 1/3
b) 1/5
c) 1/7
d) 1/9
Resposta da questão 7: [D]
Ao se lançar um
dado duas vezes há 36 possíveis resultados. Destes, apenas 4 podem ter o maior
valor menor do que 3 (1 e 1, 1 e 2, 2 e 1 e 2 e 2) Assim, a probabilidade será
igual a 4/36 = 1/9.
8. (Unicamp 2017) Um paralelepípedo retângulo tem faces de áreas 2 cm2, 3 cm2
e 4 cm2 . O volume desse
paralelepípedo é igual a :
a) 2√3 cm3
b) 2√6 cm3
c) 24 cm3
d) 12 cm3
Resposta da questão 8: [B]
Como
ab = 2, bc = 3, ac = 4 e o Volume
= a . b . c, vem
:
ab . bc . ac = 2 . 3. 4 → (a . b. c)2
= 24 → V2 = 24 → V = √24 = 2√6
9. (Unicamp 2017) Considere a circunferência de equação cartesiana x2 + y2
= x – y. Qual das equações a seguir representa uma reta que divide essa
circunferência em duas partes iguais?
a) x + y = -1
b) x - y = -1
c) x – y = 1
d) x + y = 1
Resposta da questão 9:[C]
Calculando:
x2 + y2
= x – y → (x - 1/2)2 + (y+ 1/2)2 = 1/2 → C(1/2,1/2) e R =
√2/2
A reta que divide
a circunferência em duas partes iguais passa pelo centro C e pode ter equação
igual a x – y – 1.
10. (Unicamp 2017) Considere o triângulo retângulo ABD exibido na figura abaixo, em que AB
= 2cm, BC = 1 cm e CD = 5 cm. Então, o ângulo θ é igual a :
a) 150
b) 300
c) 450
d) 600
Resposta da questão 10:[C]
Calculando: AC2 = 22 +
12 → AC = √5 e AD2 = 22 + 62
→ AD = √40
52 = (√5)2 + (√40)2
– 2.√5.√40.cosθ → 25 = 5 + 40 - 2√200.cosθ →
20 = 2√200.cosθ → cosθ = 20/2√200=20/20√2 → cosθ = √2/2
→θ = 450
11. (Unicamp 2017) Seja i a unidade imaginária, isto é, i2 = - 1. O lugar
geométrico dos pontos do plano cartesiano com coordenadas reais (x,y) tais que (2x
+ yi)(y + 2xi) = i é uma :
a) elipse.
b) hipérbole.
c) parábola.
d) reta.
Resposta da questão 11:[A]
Calculando: (2x + yi)(y + 2xi) = i → 2xy
- 2xy + (4x2 + y2)i = i
4x2 + y2 = 1 →
equação de uma elipse
12. (Unicamp 2017) Considere o polinômio p(x) = xn + xm + 1 , em que n
> m ≥ 1. Se o resto da divisão de p(x) por x + 1 é igual a 3, então :
a) n é par e m é par.
b) n é ímpar e m é ímpar.
c) n é par e m é ímpar.
d) n é ímpar e m é par.
Resposta da questão 12:[A]
O resto da divisão de p(x) por x+1 é igual a 3, portanto m e n são números pares, pois:
p(-1) = 3 → p(-1)
= (-1)n + (-1)m + 1 = 3 → logo (-1)n = (-1)m
= 1
13. (Unicamp 2017) Seja x um número real, 0 < x < π/2, tal que a sequência (tan x ,
sec x , 2) é uma progressão aritmética (PA). Então, a razão dessa PA é igual a :
a) 1
b) 5/4
c) 4/3
d) 1/3
Resposta da questão 13:[D]
Calculando: Se (tan x , sec x
, 2) e´ uma PA, entao sec x = (tan x + 2)/2.
2sec x = tan x + 2 → 2/cos x =
2 + senx/cosx → 2 = 2cosx + senx
senx = 2 -2cosx.
Como sen2x + cos2x
= 1(relaçao fundamental), vem (2-2cosx)2 + cos2x = 1
4 – 8cosx + 4cos2x + cos2x
= 1→ 5cos2x -8cosx + 3=0 → cosx = 3/5 ou
cosx = 1 (não convem) .
Portanto secx = 5/3, tgx = 4/3 e a razão da
PA e´ 1/3





Nenhum comentário:
Postar um comentário