QUESTOES VESTIBULAR G1 – ifsul 2017 – COMENTADAS.

1. (G1 - ifsul 2017)  Em uma consulta à comunidade acadêmica sobre a necessidade de melhorias na área física de um determinado campus do IFSul, foi obtido o seguinte resultado:

- 538 sugerem reformas nas salas de aula.

- 582 sugerem reformas na biblioteca.

- 350 sugerem reformas nas salas de aula e na biblioteca.

- 110 sugerem reformas em outras instalações.

Quantas pessoas foram entrevistadas nessa consulta?

a) 770   

b) 880   

c) 1120   

d) 1580   

Resposta da questão 1: [B]

Tome reforma nas salas de aula como x e reformas na biblioteca como y.

Sabendo que 350 pessoas sugerem reformas nas salas de aula e na biblioteca, ou seja, a intersecção entre x e y.

Logo, pode-se aplicar o Diagrama de Venn para tal situação da seguinte maneira:

                        

   
 

Como 350 representa a intersecção entre reformas nas salas de aula e na biblioteca, basta achar a diferença da parte das duas partes com a parte em comum. Desta forma: 538 – 350 = 188 e 582 – 350 = 232.

Transcrevendo para o Diagrama de Venn, temos:

                              

Para obter a quantidade de pessoas entrevistadas basta somar todos os valores. Note que a amostra possui 110 pessoas que opinaram reformas em outras instalações. Somando todos os valores: 188+350+232+110 = 880 pessoas.  

2. (G1 - ifsul 2017)  Em uma enquete no centro olímpico, foram entrevistados alguns atletas e verificou-se que 300 praticam natação, 250 praticam atletismo e 200 praticam esgrima. Além disso, 70 atletas praticam natação e atletismo, 65 praticam natação e esgrima e 105 praticam atletismo e esgrima, 40 praticam os três esportes e 150 não praticam nenhum dos três esportes citados. Nessas condições, o número de atletas entrevistados foi :

a) 1180   

b) 1030   

c) 700   

d) 800   

Resposta da questão 2:[C]

Utilizando o Diagrama de Venn temos:

                                

Observe que o valor 40 representa a intersecção entre as três modalidades. Como 70 é a intersecção entre natação e atletismo, temos 70 – 40 = 30. Dessa forma, como 65 é a intersecção entre natação e esgrima, e, 105 representa a intersecção entre atletismo e esgrima, temos: 65 – 40 = 25 e 105 – 40 = 65, valores a serem completados no diagrama. Logo,

                                 

 

Fazendo as diferenças das partes comuns pelo total de cada modalidade temos: 300-30-40-25 = 205, 250-30-40-65 = 115 e 200-25-40-65 = 70

Completando o diagrama, temos:

                                   

Desta maneira, para obter o total de pessoas entrevistadas, basta somar todos os valores: 205+115+70+30+40+25+65+150 = 700 pessoas entrevistadas.   

3. (G1 - ifsul 2017)  Três irmãos trabalham na mesma indústria, porém em turnos diferentes: um trabalha no intervalo das 8h às 16h, outro das 4h às 1h e o terceiro das 10h às 18h. Em qual intervalo de tempo esses irmãos trabalham juntos nessa indústria?

a) Das 4h às 18h   

b) Das 8h às 16h   

c) Das 10h às 16h   

d) Das 10h às 12h   

  

Resposta da questão 3:[D]

Para obter em qual intervalo de tempo os três irmãos trabalham juntos, deve-se fazer a intersecção entre os três intervalos (I₃) de tempo:

I₃ = [8, 16] ∩ [4, 12] ∩ [10, 18]

I₃ = [8, 12] ∩ [10, 18]

I₃ = [10, 12]

Intervalo: Das 10h às 12h.

Observe a intersecção através da reta real:

   


               

 

4. (G1 - ifsul 2017)  Uma progressão aritmética crescente é composta por 5 termos. Sabendo que o produto dos extremos é igual a 57 e que a soma dos outros 3 termos é igual a 33, determine o último termo dessa PA.

O valor encontrado é :

a) 1   

b) 3   

c) 19   

d) 57   

  

Resposta da questão 4:[C]

De acordo com a propriedade dos extremos de um PA, e, sabendo que

esta sequência possui cinco termos, temos: (a₁+a₅)/2 = (a₂+a₄)/2 = a₃

Sabe-se também que o produto dos extremos é igual a 57 e que a soma

dos outros 3 termos é igual a 33, logo: a₁ . a₅ = 57 e a₂ + a₃ + a₄ = 33

Como  (a₂+a₄)/2 = a₃, temos que a₂ + a₄ = 2 . a₃ e, podemos substituir em

a₂ + a₃ + a₄ = 33 → (2 . a₃) + a₃ = 33 → a₃₃ = 11.

E como  (a₁+a₅)/2 = (a₂+a₄)/2 = a₃ temos que a₁+a₅ = a₂+a₄ = 22

Desta maneira, pode-se reescrever o sistema da seguinte forma:

a₁ . a₅ = 57 e a₁ + a₅ = 22 → a₁ = 57/a₅ e a₁ = 22 – a₅ → a₅² – 22 a₅ + 57 = 0

Aplicando soma e produto a equação acima temos: Soma = - b/a = 22 e Produto = c/a = 57.

Logo, a₅  3 e a₅ = 19. Como o terceiro termo é a₃ = 11, descartamos a₅ = 3.

Desta forma, o quinto termo desta progressão é a₅ = 19.  

5. (G1 - ifsul 2017)  Numa serigrafia, o preço y de cada camiseta relaciona-se com a quantidade x de camisetas encomendadas, através da fórmula

y = - 0,4x + 60. Se foram encomendadas 50 camisetas, qual é o custo de cada camiseta?

a) R$ 40,00   

b) R$ 50,00   

c) R$ 70,00   

d) R$ 80,00   

Resposta da questão 5: [A]

Para obter o custo de cada camiseta, basta aplicar o valor x = 50 na função y(x) = - 0,4x + 60 → y(50) = - 0,4.50 + 60 → y(50) = 40

Portanto, R$ 40,00 cada camiseta.  

6. (G1 - ifsul 2017)  Uma função do 1º grau f : R → R possui o gráfico abaixo.

                          

A lei da função f é :

a) f(x) = x/2 + 3/2   

b) f(x) = x + 1   

c) f(x) = 2x + 1/2   

d) f(x) = x/2 + 1/2   

  

Resposta da questão 6: [D]

Para determinar a equação da reta, devemos obter o coeficiente angular

m e escolher dois pontos. Tomando os pontos (1, 1) e (7, 4) temos:

M = (4 - 1)/(7 - 1) = 3/6 = ½.

Aplicando o coeficiente angular na equação da reta (y – y₀) = m.(x – x₀) e tomando o ponto (1, 1), vem y = x/2 + 1/2

  

7. (G1 - ifsul 2017)  A equação 2^x+1 – 24 = - 64/2^x possui como solução :

a) x = 2 e x = 3   

b) x = 2 e x = 6   

c) x = 3 e x = 6   

d) x = 4 e x = 8   

Resposta da questão 7:[A]

Note que 2^x+1 = 2^x.2. Daí, temos: 2^x.2 – 24 = - 64/2^x

Fazendo a mudança de variável 2^x = y → y² + 12y + 32 = 0 → y = 4 ou y = 8

Voltando a variável original 2^x = y temos: x = 2 ou x = 3.

  

  

8. (G1 - ifsul 2017)  Uma aplicação bancária é representada graficamente conforme figura a seguir.

                          

 

M é o montante obtido através da função exponencial M = C.(1,1)^t, C  é o capital inicial e t é o tempo da aplicação. Ao final de 04 meses o montante obtido será de :

a) R$ 121,00   

b) R$ 146,41   

c) R$ 1210,00   

d) R$ 1464,10   

  

Resposta da questão 8:[D]

Para obter o montante obtido ao final de quatro meses basta aplicar t = 4 na função M(t) = C.(1,1)^t. Porém, deve-se observar o que o valor do capital inicial C, segundo o gráfico, é 1000, pois é o primeiro valor da curva exponencial. Desta forma, temos: M(4)= 1000.(,1)⁴ = 1464,10 reais

  

9. (G1 - ifsul 2017)  Uma progressão geométrica (ou PG) é uma sequência em que cada termo, a partir do segundo, é o produto do anterior por uma constante q dada.

Tendo como base a definição acima e considerando uma PG (a₁, a₂, a₃), avalie as seguintes afirmações:

I. A progressão geométrica pode ser escrita como (x-q, x, x+q).

II. O termo a₂ pode ser escrito como a₂ = √a₁.a₃

III. É válida a relação a₂/a₁ = a₃/a₂ .

IV. Se q < 0, a PG será decrescente.

Estão corretas as afirmativas

a) I e II apenas.   

b) I, III e IV apenas.   

c) II e III apenas.   

d) I, II, III e IV.   

Resposta da questão 9:[C]

[I] Incorreta, pois a expressão (x – q, x, x +q) representa uma progressão aritmética.

[II] Correta, pois, seja uma PG = a₁, a₂, a₃, ... onde o primeiro termo é a₁ e a razão é q temos: PG = a₁, a₁.q, a₁.q², ...

    Aplicando a média geometria na PG, temos: a₁.q = √(a₁)( a₁.q²) = a₁ .q

    Como a₁ . q = a₂ e a₁ . q² = a₃ temos: a₂ = √ (a₁ . a₃)

[III] Correta, pois como trata-se de uma progressão onde, uma razão q deve ser multiplicada pelo termo anterior para se obter um novo termo, a razão entre dois termos consecutivos deve ser sempre a mesma. Ou seja: a₂/ a₁ = q → a₂ / a₁ = a₃ / a₂

[IV] Incorreta, pois uma razão negativa pode tornar a sequência alternada, ou seja, a mesma pode alternar entre valores positivos e negativos.

Tome uma PG com primeiro termo a₁ = 1 e razão q = -1 →PG = 1, -1, 1,...

Note que a sequência se alterna infinitamente e não é necessariamente decrescente.  

10. (G1 - ifsul 2017)  A temperatura da cidade de Porto Alegre – RS foi medida, em graus Celsius, três vezes ao dia, durante 6 dias. Cada elemento a_ij da matriz

                           

corresponde à temperatura observada no tempo i do dia j. Com base nos dados da matriz A, analise as seguintes proposições:

I. A temperatura mínima registrada está na posição a₁₂

II. A maior variação de temperatura registrada entre os tempos 1 e 2 aconteceu no primeiro dia.

III. A temperatura máxima registrada está na posição a₃₄

Estão corretas as afirmativas

a) I e III apenas.   

b) I e II apenas.   

c) II e III apenas.   

d) I, II e III.   

  

Resposta da questão 10: [D]

[I] Correta, pois, a temperatura registrada na posição a₁₂ é o menor valor dentre todos os valores presentes na matriz. Ou seja, 8,1 = a₁₂ < a_ij, i ǂ 1 e j ǂ 2.

[II] Correta, pois, a maior variação entre os tempos 1 e 2 está registrada no primeiro dia. Observe que as variações do primeiro ao sexto dia, respectivamente são: 2,8 , 2,4 , 2,6 , 2,5 , 1,2 , 1,4, . Logo, a maior variação é 2,8 respectivo ao primeiro dia.

[III] Correta, pois a temperatura registrada na posição a₃₄ é o maior valor dentre todos os valores presentes na matriz. Ou seja, 21 = a₃₄ > a_ij, i ǂ 3 e j ǂ 4.

11. (G1 - ifsul 2017)  O Brasil foi pioneiro na utilização de carros bicombustíveis, ou seja, veículos que podem ser abastecidos com gasolina ou com álcool. Considere que, em um determinado posto de combustíveis, o preço de 2 litros de gasolina com mais  litros de álcool é R$ 20,00. Também sabe-se que 1 litro de gasolina juntamente com 12 litros de álcool é vendido por R$ 40,00. É correto afirmar que, nesse posto, cada litro de álcool custa:

a) R$ 2,50   

b) R$ 3,00   

c) R$ 3,50   

d) R$ 4,00   

  

Resposta da questão 11:[B]

Seja gasolina denominada por x e álcool por y.

Sabemos que o preço de 2 litros de gasolina com mais 4 litros de álcool é

R$20,00, isto é: 2x + 4y = 20 → x + 2y = 10

Sabemos também que 1 litro de gasolina juntamente com 12 litros de

álcool é vendido por R$40,00, isto é: x + 12y = 40.

Para obtermos o valor de cada litro de álcool devemos resolver ambas as

equações através de um sistema da seguinte maneira: x + 2y = 10

e x + 12y = 40 → y = 3 e x = 4. Logo, o valor do litro de álcool é de R$3,00  

12. (G1 - ifsul 2017)  Durante os séculos 18 e 19, muitos matemáticos se destacaram por suas contribuições na área da matemática. Dentre eles está Carl Friedrich Gauss (1777–1855) que ficou conhecido como "o príncipe da matemática" ou "o mais notável dos matemáticos" e seu trabalho teve enorme importância principalmente em áreas como a teoria da probabilidade. De posse dessa teoria, duas pessoas, A e B, decidem lançar um par de dados. Eles combinam que se a soma dos números dos dados for 7, A ganha, e se a soma for 10, B ganha. Cada par de dados é lançado uma única vez. A probabilidade de B ganhar é de :

a) 1/6   

b) 1/2   

c) 1/36   

d) 1/12   

  

Resposta da questão 12:[D]

Para que B vença, as possíveis combinações dos dois dados devem ser:

4 + 6 ou 5 + 5 ou 6 + 4.

Observe que a probabilidade de se lançar um dado e cair um número ao

acaso é 1/6, visto que um dado possui seis faces. Desta forma, as

probabilidades P(x) são o produto de ambas as possibilidades de se obter

a soma desejada. Ou seja, P(4+6) = P(5+5) = P(6+4) = 1/6.1/6 = 1/36 

Logo, somando as possíveis probabilidades temos:

P(4+6) + P(5+5) + P(6+4) = 1/36  + 1/36   + 1/36 = 1/12

  

13. (G1 - ifsul 2017)  As raízes das equações 5x – 2 = 3x + 6 e (y - 1).(y + 4) = y² + 5 representam as medidas dos comprimentos dos catetos do triângulo retângulo da figura, representada a seguir.

                                   

Assim, o comprimento da hipotenusa z desse triângulo retângulo é :

a) 4   

b) 5   

c) 6   

d) 7   

    

Resposta da questão 13: [B]

Obtendo as raízes das equações: 5x – 2 = 3x + 6 → x = 4

(y - 1).(y + 4) = y² + 5 → 3y = 9 → y = 3

Como os valores dos catetos são 4 e 3, aplicando o Teorema de Pitágoras

temos: z² = 4² + 3² → z = 5

  

14. (G1 - ifsul 2017)  As medidas do comprimento e da altura (em metros) do outdoor retangular, representado na figura abaixo, são exatamente as soluções da equação x² – 10x + 21 = 0.

        

Dessa forma, é correto afirmar que a área desse outdoor é :

a) 10 m²   

b) 20 m²   

c) 21 m²   

d) 24 m²   

  

Resposta da questão 14:[C]

Obtendo as raízes de x² – 10x + 21 = 0, através da Fórmula de Bhaskara,

temos: x = 3 ou x = 7.  Logo, como a área do outdoor é dada pelo produto

de seus lados, temos: 21 m².  

15. (G1 - ifsul 2017)  O projeto de madeiramento é fundamental para a construção de um bom telhado em uma residência.

Na figura, temos a vista frontal do madeiramento de um telhado. O triângulo ABC é isósceles de base C tal que A = 120⁰. Observa-se também que os segmentos DE e FG são perpendiculares à base BC.

                   

                  

De acordo com os dados acima, a medida do ângulo é BED é :

a) 30⁰   

b) 45⁰   

c) 60⁰   

d) 75⁰   

  

Resposta da questão 15:[C]

Como o triângulo ABC é isósceles e o ângulo BAC = 120⁰ os ângulos ABC

= ACB = 30⁰. Logo, como  ABC = 30⁰ e os segmentos DE e FG são

perpendiculares à base BC, ou seja, formam um ângulo reto entre a base   

e os segmentos, o ângulo BDE oposto pelo vértice DE, também é reto .

Desta maneira, para obter o valor de x, deve-se somar todos ângulos do

triângulo BDE : x + BDE + EBD = 180⁰→ x + 90⁰ + 30⁰ = 180⁰ → x = 60⁰

  

16. (G1 - ifsul 2017)  O ano de 2016 ficará marcado na história do Brasil pelo fato de o Rio de Janeiro ter sediado o maior evento esportivo do mundo: as Olimpíadas. Aproveitando o tema, um grupo de estudantes construiu os 5 anéis olímpicos, conforme figura, reaproveitando mangueiras usadas. Cada aro construído mede 80 cm de diâmetro.

                       

Considerando os dados acima, a medida, em metros, do total de mangueiras utilizadas nesse trabalho, é :

a) 2π   

b) 4π   

c) 8π   

d) 16π   

  

Resposta da questão 15:[C]

Como o triângulo ABC é isósceles e o ângulo BAC = 120⁰ os ângulos ABC

= ACB = 30⁰. Logo, como  ABC = 30⁰ e os segmentos DE e FG são

perpendiculares à base BC, ou seja, formam um ângulo reto entre a base   

e os segmentos, o ângulo BDE oposto pelo vértice DE, também é reto .

Desta maneira, para obter o valor de x, deve-se somar todos ângulos do

triângulo BDE : x + BDE + EBD = 180⁰→ x + 90⁰ + 30⁰ = 180⁰ → x = 60⁰

  

Resposta da questão 16:[B]

Sabendo que o comprimento C de uma circunferência é dado por c = 2.π.r e que o diâmetro D representa o dobro do raio r de cada circunferência, temos: D = 2r → r = 40 cm.

Logo, o comprimento de cada anel é dado por: C = 2 . π . 40 = 0,8π m

Assim, basta multiplicar o comprimento de cada anel pelo número total de

anéis (cinco). Desta maneira: 0,8π . 5 = 4π m.

  

17. (G1 - ifsul 2017)  Analise a tirinha abaixo.

De acordo com a tirinha, o triângulo é classificado como :

a) retângulo.   

b) equilátero.   

c) isósceles.   

d) escaleno.   

  

Resposta da questão 17:[B]

De acordo com a fala da professora no quinto quadrinho da tirinha “Um triangulo cujos lados são todos iguais” pode-se afirmar que trata-se de um triângulo equilátero. Lembrando da classificação dos triângulos, quanto aos lados, temos:

1) Equilátero: os três lados do triângulo possui medidas iguais;

2) Isósceles: possui dois lados com medidas iguais e um lado com medida diferente;

3) Escaleno: os três lados possuem medidas diferentes  

18. (G1 - ifsul 2017)  A produção de lixo representa um importante tema ambiental. Cada pessoa de uma certa cidade com 72000 habitantes produz, em média, 3/4 kg de lixo por dia. Para o transporte do lixo, da cidade ao aterro sanitário, é utilizado um caminhão cuja capacidade de carga corresponde a 9000 kg. Dessa forma, é correto afirmar que o número de caminhões que podem ser carregados com o lixo produzido diariamente nessa cidade é :

a) 6   

b) 7   

c) 8   

d) 9   

  

Resposta da questão 18:[A]

Sabendo que cada habitante produz em média 3/4 kg de lixo por dia e a

cidade possui 72000 habitantes, deve-se obter quantos quilos de lixo a

cidade produz. Desta maneira, temos a seguinte proporção:

1/(3/4) = 72000/x, onde x representa o total de lixo produzido pela cidade.

Resolvendo a equação: x = 54000kg

Para se obter o número de caminhões utilizados basta dividir, o total de

quilos de lixo produzido pela capacidade de carga de cada caminhão:

54000/9 = 6 caminhões.  

19. (G1 - ifsul 2017)  Em uma indústria metalúrgica, 4 equipamentos operando 8 horas por dia durante 5 dias, produzem 4 toneladas de certo produto. O número de dias necessários para produzir 3 toneladas do mesmo produto por 5 equipamentos do mesmo tipo, operando 6 horas por dia é :

a) 3   

b) 4   

c) 5   

d) 6   

  

Resposta da questão 19:[B]

Observe a tabela com os dados:

Equipamentos	Horas	Dias	Produção
4	8	5	4
5	6	x	3

Note que:

1) O número de equipamentos é inversamente proporcional ao número de dias, pois, quanto maior o número de equipamentos na produção, menor o número de dias para realizar a produção;

2) O número de horas é inversamente proporcional ao número de dias, pois, quanto maior o número de dias a ser utilizado na produção, pode-se diminuir o número de horas de produção por dias;

3) A quantidade de toneladas do produto produzido é diretamente proporcional ao número de dias, ou seja, quanto mais dias operando, maior a produção.

Logo, aplicando a regra de três composta: 5/x = 5/4 . 6/8 . 4/3 →

x = 4 toneladas.  

20. (G1 - ifsul 2017)  Médicos recomendam o consumo moderado de refrigerante, visto a quantidade elevada de açúcares presente nesse tipo de bebida. Observe os dados nutricionais de uma lata de refrigerante, conforme representado em tabela abaixo.

INFORMAÇÕES NUTRICIONAIS PARA PORÇÃO DE 350 Ml (2 copos)
Quantidade por porção		% Valor diário
Valor energético	149kcal = 624 kj	7
Açúcares	37g	12
Sódio	18mg	1

Considerando os dados da tabela, a quantidade aproximada de açúcares, em gramas, presente em 1 litro desse refrigerante, é :

a) 105,7   

b) 109,5   

c) 117,3   

d) 157,1   

Resposta da questão 20:[A]

De acordo com a tabela, observa-se que 350ml de refrigerante possui 37g

de açucares, logo, para analisarmos quantas gramas de açucares estão

presentes em um litro 1000ml utilizamos a seguinte proporção:

350/37 = 1000/x , onde x representa a quantidade de gramas em um litro

de refrigerante, x ≈ 105,7g.

21. (G1 - ifsul 2017)  Visando economizar energia elétrica, uma pessoa substituiu lâmpadas fluorescentes de 25 W por lâmpadas LED de 16 W.

Em termos percentuais, a economia de energia elétrica, em cada troca de lâmpada, será de :

a) 25%   

b) 32%   

c) 36%   

d) 41%   

  

Resposta da questão 21:[C]

Para obtermos o percentual economizado, devemos calcular qual a

porcentagem que 16w representa dentro dos 25w. Logo, temos a seguinte

proporção: 25/100% = 16/x% ,  onde x representa a porcentagem

procurada, → x = 64%

Nesse sentido, 16W representa 645 dos 25W. Logo, devemos apenas

subtrair as porcentagens para obter o percentual relativo à economia:

100% - 64% = 36%.  

22. (G1 - ifsul 2017)  As corridas com obstáculos são provas de atletismo que fazem parte do programa olímpico e consistem em corridas que têm no percurso barreiras que os atletas têm de saltar. Suponha que uma prova tenha um percurso de 1000 metros e que a primeira barreira esteja a 25 metros da largada, a segunda a 50 metros, e assim sucessivamente.

Se a última barreira está a 25 metros da linha de chegada, o total de barreiras no percurso é :

a) 39   

b) 41   

c) 43   

d) 45   

Resposta da questão 22:[A]

Para obter o número total de barreiras, basta dividir o tamanho total do

percurso pelo espaço que cada barreira está uma da outra, ou seja,

1000 ÷ 25 = 40. Porém, como a última barreira está a 25 metros da linha de

chegada, deve-se subtrair uma barreira, logo: 40 – 1 = 39 barreiras.  

23. (G1 - ifsul 2017)  Segundo o Censo Demográfico de 2010, a população das regiões do Brasil foi identificada conforme tabela abaixo:

Região	População
Norte	15865678
Nordeste	53078137
Sudeste	80353724
Sul	27384815
Centro-Oeste	14050340

Ordenando as populações de forma crescente, as regiões ficariam assim elencadas:

a) Centro-Oeste, Nordeste, Norte, Sudeste, Sul.   

b) Centro-Oeste, Norte, Sul, Nordeste, Sudeste.   

c) Centro-Oeste, Sudeste, Sul, Nordeste, Norte.   

d) Centro-Oeste, Sul, Sudeste, Nordeste, Norte.   

  

Resposta da questão 23: [B]

Ordenando em ordem crescente (menor valor ao maior valor):

14050340 > 15865678 > 27384815 > 53078137 > 80353724

Centro-Oeste, Norte, Sul, Nordeste, Sudeste.  

24. (G1 - ifsul 2017)  Considere as expressões numéricas abaixo.

A = - 10 + 6 . 4   e   B = 2⁵ - √64. É correto afirmar que o valor de A+B é :

a) 8   

b) 16   

c) 26   

d) 38   

  

Resposta da questão 24: [D]

Resolvendo as expressões:

A = - 10 + 6.4 = 14  e  B = 2⁵ - √64 = 24. Logo A + B = 38

  

25. (G1 - ifsul 2017)  O valor numérico da expressão E = (xy²-xy)/(x³-x), para x = 4 e y = - 3, é :

a) - 1/5   

b) 2/5   

c) - 3/5   

d) 4/5   

Resposta da questão 25:[D]

Substituindo os valores x = 4 e y = - 3 na expressão temos:

E = [4 .(-3)² – 4.(-3)]/(4³- 4) = 48/60 = 4/5

  

TEXTO PARA A PRÓXIMA QUESTÃO:

A doença do amor

Luiz Felipe Pondé

            Existe de fato amor romântico? Esta é uma pergunta que ouço quando, em sala de aula, estamos a discutir questões como literatura romântica dos séculos 18 e 19. ¹Quando o público é composto de pessoas mais maduras, a tendência é um certo ceticismo, muitas vezes elegante, apesar de trazer nele a marca eterna do desencanto.

            Quando o público é mais ²jovem há uma tendência maior de crença no amor romântico. ³Alguns diriam que ⁴essa crença é típica da idade jovem e inexperiente, assim como crianças creem em Papai Noel.

            Mas, em matéria de amor romântico, melhor ainda do que ir em busca da literatura dos séculos 18 e 19 é ir ⁵à fonte primária ⁶: a literatura europeia medieval, verdadeira fonte do amor romântico. A literatura conhecida como amor cortês.

            Especialistas no assunto, como o suíço Denis de Rougemont, suspeitavam que a literatura medieval criou uma verdadeira expectativa neurótica no Ocidente sobre o que seria o amor romântico em nossas vidas concretas, fazendo com que ⁷sonhássemos com algo que, na verdade, nunca existiu como experiência universal. ⁸Dos castelos da Provence francesa do século 12 ao cinema de Hollywood, teríamos perdido o verdadeiro sentido do amor medieval, que seria uma doença da qual devemos fugir como o diabo da cruz.

            Para além dos céticos e crentes, a literatura medieval de amor cortês é marcante pela sua descrição do que seria esse pathos amoroso. Uma doença, uma verdadeira desgraça para quem fosse atingindo em seu coração por tamanha tristeza. André Capelão, autor da época ("Tratado do Amor Cortês", ed. Martins Fontes), sintetiza esse amor como sendo uma ⁹"doença do pensamento". Doença essa que podemos descrever como uma forma de obsessão em saber o que ela está pensando, o que ela está fazendo nessa exata hora em que penso nela, com o que ela sonha à noite, como é seu corpo por baixo da roupa que a veste, o desejo incontrolável de ouvir sua voz, de sentir seu perfume. Mas a doença avança: sentir o gosto da sua boca, beijá-¹⁰la por horas a fio.

            ¹¹Mas, quando em público, jamais deixe ninguém saber que se amam. Capelão chega a supor que desmaios femininos poderiam ser indicativos de que a infeliz estaria em presença de seu desgraçado objeto de amor inconfessável. A inveja dos outros pelos amantes, apesar de ¹²condenados a ¹³tristeza pela interdição sempre presente nas narrativas (casados com outras pessoas, detentores de responsabilidades públicas e privadas), se dá pelo fato que se trata de uma doença encantadora quando correspondida.

            Nada é mais forte do que o desejo de estar com alguém a quem você se sente ligado, mesmo que a milhares de quilômetros de distância, sem poder trocar um único olhar ou toque com ela.

            O erro dos modernos românticos teria sido a ilusão de que esses medievais imaginariam o amor romântico numa escala universal e capaz de ¹⁴conviver com um apartamento de dois quartos, pago em cem anos.

            Não, o amor cortês seria algo que deveríamos temer justamente por seu caráter intempestivo e avassalador. Sempre fora do casamento, teria contra ele a condenação da norma social ou religiosa que, aos poucos, ¹⁵levaria as suas vítimas à destruição, psicológica ou física.

            Para os medievais, um homem arrebatado por esse amor tomaria decisões que destruiriam seu patrimônio. A mulher perderia sua reputação. Ambos viriam, necessariamente, a morrer por conta desse amor, fosse ele em batalha, por obrigação de guerreiro, fosse fugindo do horror de trair seu melhor amigo com sua até então fiel esposa. Ela morreria eventualmente de tristeza, vergonha e solidão num convento, buscando a paz de espírito há muito perdida. A distância física, social ou moral, proibindo a realização plena desse desejo incessante como tortura cotidiana.

            O poeta mexicano Octavio Paz, que dedicou alguns textos ao tema, entendia que a literatura medieval descrevia o embate entre virtude e desejo, sendo a desgraça dos apaixonados a maldição de ter que ¹⁶pôr medida nesse desejo ¹⁷(nesse amor fora do lugar), em meio à insuportável culpa de estar doente de amor.

Texto adaptado. Foi publicado em 16 de maio de 2016 na Folha de S. Paulo. Disponível em:

<http://www1.folha.uol.com.br/colunas/luizfelipeponde/2016/05/1771569-a-doenca-do-amor.shtml>. Acesso em: 21 set. 2016.

26. (G1 - ifsul 2017)  Observando o segundo parágrafo do texto A doença do amor, o número de anagramas (qualquer permutação das letras de uma palavra de modo a formar ou não novas palavras) que podemos formar com a palavra escrita imediatamente após "idade", é :

a) 120   

b) 24   

c) 720   

d) 20

Resposta da questão 26:[A]

A palavra após “idade” é a palavra “jovem”, que possui cinco letras distintas. Logo, o número de anagramas  que a palavra “jovem” possui é: 5! = 120.  

TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:

Utilize o fragmento de texto abaixo para responder à(s) questão(ões).

O salário total ST(x) de um funcionário de certa empresa é composto de duas partes, uma fixa no valor de R$ 1230,0 e outra que varia de acordo com a função s(x) = 10x + det A, sendo x o tempo de serviço, em anos, do funcionário na empresa, com

                                    

27. (G1 - ifsul 2017)  O salário total do funcionário que trabalha há três anos nesta empresa é :

a) R$ 1296,00   

b) R$ 1324,00   

c) R4 1318,00   

d) R$ 1300,00   

  

Resposta da questão 27: [C]

Para obter o salário de um funcionário que trabalha há três anos basta

calcular ST(x) = 7x² + 8x + 1231→ ST(3) = 7(3)² + 8(3) + 1231→ 1318 reais

28. (G1 - ifsul 2017)  A função que descreve o salário total do funcionário é :

a) ST(x) = 7x² + 8x + 1231   

b) ST(x) = 7x² + 10x + 1230   

c) ST(x) = 7x² + 10x + 1231   

d) ST(x) = 7x² + 8x + 1230   

Resposta da questão 28:[A]

Para obter a função que descreve o salário total do funcionário, basta calcular o valor do determinante da matriz e somá-lo ao salário fixo. Desta forma, utilizando o Método de Sarrus para o cálculo de determinantes, tem-se que:

                  

Somando s(x) + 1230 para obter ST(x) temos:

ST(x) = 10x + detA + 1230 → ST(x) = 7x² + 8x + 1231

  

29. (G1 - ifsul 2017)  O gráfico abaixo apresenta a taxa de analfabetismo de pessoas de 15 anos ou mais de idade, por sexo, no Brasil.

              

De acordo com o gráfico, analise as seguintes afirmações:

I. O número de homens analfabetos em 2007 é menor do que em 2009.

II. O número de mulheres analfabetas diminui de 2007 a 2015.

III. O número de analfabetos em 2009 é maior do que em 2011.

Estão corretas as afirmativas  

a) I e III apenas.    

b) I e II apenas.    

c) II e III apenas.    

d) I, II e III.    

  

Resposta da questão 29: [C]

[I] Incorreta. É maior. Note que o ano de 2007 está muito mais acima da linha de referência que o ano de 2009.

[II] Correta. Note que o ano de 2007 está acima da linha de 9,0 e o ano de 2015 está abaixo.

[III] Correta. Note que o ano de 2009 está acima da linha de 9,0 e o ano de 2011 está abaixo.  

30. (G1 - ifsul 2017)  Analisando os conteúdos nos quais os alunos possuem maiores dificuldades de aprendizagem em uma escola com 500 alunos, percebeu-se que: 208, têm dificuldades de aprendizagem em matemática; 198, em português; 154, em física; 62, em matemática e física; 38, em português e física; 52, em matemática e português e 20 têm dificuldades nas três disciplinas. Por esse viés, o número de alunos que não tem dificuldades em nenhuma dessas disciplinas é de  :

a) 92 alunos.    

b) 72 alunos.    

c) 60 alunos.    

d) 20 alunos.    

  

Resposta da questão 30: [B]

Utilizando o diagrama de Venn temos:

                    

  

Subtraindo o total de cada matéria pelas intersecções temos:

                              

Logo, somando todos os valores e subtraindo 500 temos: 500 – 428 = 72

  

31. (G1 - ifsul 2017)  Em uma disciplina, o número de alunos reprovados por ano é descrito pela função g(t), em que t é dado em anos. Considerando f(g(t)) = √(2t + 1) e f(t) = √(t - 2), é possível afirmar que a função g(t) é :

a) g(t) = 2t + 3   

b) g(t) = √(2t + 3)   

c) g(t) = 2t - 3      

d) g(t) = √(2t - 3)      

  

Resposta da questão 31:[A]

Aplicando g(t) em f(t) temos: f(t) = √(t - 2) →

f(g(t)) = √(g(t) - 2) → √(2t + 1) = √(g(t) - 2)

Elevando ambos lados ao quadrado para extrair as raízes temos:

2t + 1 = g(t) – 2 → g(t) = 2t + 3

  

32. (G1 - ifsul 2017)  Na última páscoa, a direção de um campus do IFSul solicitou que cada servidor doasse caixas de bombons para serem entregues a 16 000 alunos de baixa renda das escolas da região. Supondo-se que o primeiro servidor doou uma caixa; o segundo doou 2, o terceiro, 4 e assim sucessivamente até o décimo quinto servidor, é possível afirmar que o total de caixas de bombons arrecadadas foi suficiente para doar exatamente :

a) uma para cada aluno.    

b) duas para cada aluno.    

c) uma para cada aluno e ainda sobraram 767 caixas de bombons.    

d) duas para cada aluno e ainda sobraram 767 caixas de bombons.    

  

Resposta da questão 32:[D]

De acordo com as doações, as doações seguem um padrão de

progressão geométrica, assim, basta obter a soma desta progressão de

primeiro termo a₁ = 1, e razão r = 2 temos: S₁₅ = a₁(rⁿ - 1)/(r - 1) =

1.(2ⁿ - 1)/(2 - 1) = (2ⁿ - 1)/1= 32767 caixas de bombom doadas.

Logo, cada aluno receberá duas caixas (2 . 16000 = 32000 e sobrarão 767

caixas.  

33. (G1 - ifsul 2017)  As idades de um casal são caracterizadas por dois números naturais desconhecidos, x e y. A soma das idades desse casal é de 64 anos e a diferença das idades é de 2 anos.

Dessa forma, é correto afirmar que o produto das idades é :

a) 1021   

b) 1022   

c) 1023   

d) 1024   

  

Resposta da questão 33:[C]

Admitindo a situação temos o seguinte sistema: x + y = 64 e x – y = 2,

2x = 66 → x = 33 e y = 31.

Obtendo o produto temos: xy = 31.33 = 1023

  

34. (G1 - ifsul 2017)  O número de anagramas distintos que podemos formar com o termo DIREITO é :

a) 5040   

b) 2520   

c) 120   

d) 7   

  

Resposta da questão 34:[B]

Como a palavra DIREITO possui sete letras com a letra I repetida duas

vezes, basta aplicar a fórmula da permutação com repetições. Logo:

P₇² = 7!/2! = 5040/2 = 2520 anagramas.  

35. (G1 - ifsul 2017)  Considerando o termo “neves”, podemos afirmar que a probabilidade de escolhermos uma letra ao acaso deste termo e esta ser uma vogal é :

a) 1/4   

b) 1/2   

c) 1/5   

d) 2/5   

  

Resposta da questão 35: [D]

Basta dividirmos o número de ocorrências, pelo número total de letras. Neste caso, tem-se apenas a vogal “e” que aparece duas vezes em uma palavra de cinco letras, logo: P = 2/5

 

36. (G1 - ifsul 2017)  Após trabalhar os conteúdos de área e volume de figuras espaciais, o professor de matemática sugeriu um exercício, utilizado por Técnicos em Mecânica, para que os alunos percebessem uma das aplicações desses conteúdos. Nesse contexto, solicitou para os alunos calcularem o módulo do resfriamento de um cilindro.

Sabendo-se que o módulo do resfriamento é a divisão do volume total do cilindro pela sua área total, afirma-se que o módulo do resfriamento do cilindro fechado (com tampa) da figura abaixo é :

                         

a) 169,56 cm   

b) 54 cm   

c) 1,2 cm   

d) 1 cm   

  

Resposta da questão 36:[D]

Sabendo que o volume é dado pelo produto entre a área da base e a altura

temos: V = 3².π.6 = 54π.

E a área total é a soma da área lateral (retangular) e as áreas da base e

superior (áreas de um círculo) temos: A = 2.π.3.6 + 2.π.3² = 54π.

Dividindo: 54π/54π = 1

  

37. (G1 - ifsul 2017)  Na reta a seguir, a distância entre quaisquer dois pontos consecutivos é a mesma.

                             

Considerando que a unidade de medida de x é em metros, o valor da distância é :

a) 4 m   

b) 5 m   

c) 6 m   

d) 7 m   

  

Resposta da questão 37:[A]

Como a distância entre quaisquer dois pontos consecutivos é a mesma,

podemos subtrair os pontos da seguinte maneira:

3x – 2x = x² – 3x →x² – 4x = 0 → x' = 0 e x'' = 4

Como a distancia é necessariamente maior que zero temos: x = 4 metros.  

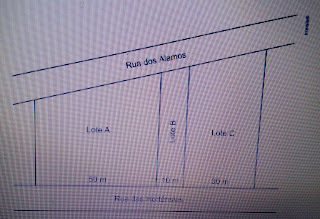
38. (G1 - ifsul 2017)  Três lotes residenciais têm frente para a rua dos Álamos e para a rua das Hortênsias, conforme a figura a seguir.

                        

As fronteiras entre os lotes são perpendiculares à rua das Hortênsias. Qual é a medida, em metros, da frente do lote A para a rua dos Álamos, sabendo-se que as frentes dos três lotes somadas medem 135 metros ?

a) 55   

b) 65   

c) 75   

d) 85   

  

Resposta da questão 38:[C]

Considere a situação descrita:

                                                        

Como sabemos que x + y + z = 135 metros, aplicando o teorema de Talles

temos a seguinte proporção: 90/135 = 50/x → x = 75.

39. (G1 - ifsul 2017)  Em uma escola, o professor de matemática levou seus alunos para o pátio e solicitou que cada um observasse em sua volta e posteriormente elaborasse um exercício envolvendo o conteúdo de geometria com o que haviam avistado. Um dos exercícios construído foi o cálculo da área de uma nuvem formada por três semicírculos idênticos conforme a figura abaixo.

                                  

Para desenvolver o cálculo, foi utilizado π = 3,14. Com isso, afirma-se que a área da nuvem é aproximadamente :

a) 90,88 cm²   

b) 84,44 cm²      

c) 64,88 cm²      

d) 61,44 cm²      

  

Resposta da questão 39:[D]

Considere a situação:

                                      

 

Desta maneira, a área da nuvem será dada pela área dos três semicírculos de raio 5 centímetros somadas com a área do trapézio interior. Porém, deve-se obter a altura h do trapézio através do teorema de Pitágoras, logo:

                                                   

hip² = cat² + cat² → 5² = h² + 3² → 25 = h² + 9 → h² = 25 – 9 → h = 4 cm

Desta maneira, a área da nuvem é dada por:

A = 3.πr²/2 + (B + b)h/2 = 3.π.(5/2)²/2 + (11 + 5)4/2 = 3.3,14.25/8 + (11 + 5)4/2

A = 29,43 + 32 = 61,43 cm²

40. (G1 - ifsul 2017)  A figura a seguir representa a sala de estar de um apartamento.

                                 

A quantidade mínima necessária de piso flutuante, em metros quadrados, para cobrir todo o chão da sala é:

a) 20   

b) 21   

c) 22   

d) 23   

  

Resposta da questão 40:[D]

De acordo com a figura temos:

                         

Assim, basta calcular a área em metros quadrados. A área será dada pela soma dos dois retângulos. Logo: 5.4 + 3.1 = 20 + 3 = 23 m²

  

41. (G1 - ifsul 2017)  Um objeto de decoração tem a forma de um  pentágono regular, apresentando todas as suas diagonais. Sabe-se que cada diagonal foi pintada de uma cor diferente das demais. Então, qual é o número de cores diferentes que foram utilizadas na pintura de tais diagonais? 

a) 5   

b) 6   

c) 8   

d) 9   

  

Resposta da questão 41:[A]

Contando as diagonais temos:

                                          

Cinco diagonais.  

42. (G1 - ifsul 2017)  De uma forma criativa, após um exame, o professor entregou as notas expressas por números complexos aos seus alunos. Para cada aluno descobrir sua nota, era necessário calcular o módulo (observe que o módulo de um número complexo z = a + bi é calculado por |z| = √(a² + b²) do número complexo descrito no seu exame.

Dessa forma, as notas representadas pelos números complexos

N₁ = 4.(cos2π/3 + i.sen2π/3), N₂ = 3.(cos5π/6 + i.sen5π/6) e

N₃ = (5/2 + i).(1/2 - i) – 3i/4  aproximados são, respectivamente,

a) 4; 3 e 3,5   

b) 3; 4 e 3,5   

c) 3; 4 e 5   

d) 4; 3 e 5   

  

Resposta da questão 42:[A]

Observa-se que as notas N₁ e N₂ estão representadas na forma

trigonométrica, assim, os valores 4 e 3 são os valores dos módulos e

consequentemente das notas.

Nota-se que um número complexo representado na forma trigonométrica

é z = |z|.(cosƟ + i.senƟ).

Logo, basta calcular o módulo de N₃  .

N₃  = (5/2 + i).(1/2 - i) – 3i/4 = 5/2.1/2 – 5i/2 + i/2 – i² – 3i/4 = 5/4 – 11i/4 + 1 →

N₃ = 9/4 – 11i/4 → | N₃ | = √[(9/4)² + (11/4)²] ≈ 3,5

  

43. (G1 - ifsul 2017)  Para se fabricar 20 camisas iguais são necessários 30 metros de um certo tecido. Quantos metros do mesmo tecido serão necessários para fabricar 50 camisas iguais às citadas?

a) 45   

b) 55   

c) 65   

d) 75   

  

Resposta da questão 43:[D]

Segundo a situação temos a seguinte proporção: 20/30 = 50/x →

20x = 1500 → x = 75 metros.  

  

44. (G1 - ifsul 2017)  Segundo uma pesquisa realizada em uma determinada cidade, numa população de 6000 habitantes foi estimado que 1920 pessoas são aposentadas.

Qual é a porcentagem de aposentados nessa cidade?

a) 31%   

b) 32%   

c) 33%   

d) 34%   

  

Resposta da questão 44:[B]

Basta dividirmos o numero de aposentados pelo número total da

população: 1920/6000 = 0,32 = 32%

45. (G1 - ifsul 2017)  A figura a seguir representa a área de um jardim com o formato de um triângulo retângulo isóscele. Nele deverá ser colocada uma tela para cercar totalmente o terreno.

                                 

Considerando os dados apresentados, quantos metros de tela, no mínimo, serão necessários?

a) 4√2 + 2   

b) 2√2 + 2   

c) 4√2   

d) 2√2   

  

Resposta da questão 45:[B]

Do fato do triangulo ser isósceles, os dois outros ângulos serão de 45⁰ e

então, basta aplicar o teorema de Pitágoras para obter o valor dos dois

lados que serão iguais. Logo: sen 45⁰ = cos 45⁰ = √2/2 → cat. = √2

Obtendo o perímetro (soma de todos os lados) temos: 2 + √2 + √2 =

= 2 + 2√2

46. (G1 - ifsul 2017)  Para assar um peru são necessários 12 minutos para aquecer o forno e mais 22 minutos para assar um quilo de peru. Sabendo-se que o forno está frio, é correto afirmar que o tempo mínimo, em minutos, para assar um peru de 3,5 kg é de :

 

a) 79   

b) 89   

c) 99   

d) 109   

  

Resposta da questão 46:[B]

Temos que somar o tempo de aquecimento do forno mais o produto do

tempo de cada quilo com o total de quilos do peru, logo: 12 + 3,5.22 = 89

minutos.  

47. (G1 - ifsul 2017)  O valor numérico da expressão x⁴ – 2x² + 3, quando   x = 1/√2, é :

a) 3/16   

b)√2/2   

c) 9/4   

d) (2√2)/3   

Resposta da questão 47:[C]

Substituindo, temos: x⁴ – 2x² + 3 = (1/√2)⁴ – 2(1/√2)² + 3 = 1/4 - 1 + 3 = 9/4