1. Um prisma reto tem por base um losango em que uma
das diagonais mede 3/4 da outra, e a soma de ambas é 14 cm. Calcule a área
total e o volume desse prisma, sabendo que sua altura é igual ao semiperímetro
da base.
Resolução :
Se d = 3D/4 e D + d = 14 → D + 3D/4 = 14 → 4D + 3D = 56 → 7D = 56 →
D = 8 cm e d = 3D/4 = 3.8/4 = 6 cm
Lado do losango → l2 = (D/2)2 +
(d/2)2 → l2 = (8/2)2 + (6/2)2 → l =
5 cm
H = semiperímetro da base → p = 2l = 10 cm
Área total = 2.Área da base + Área lateral = 2.(D.d)/2
+ 4.l.H =
2.8.6/2 + 4.5.10 = 48 + 200 → ATotal
= 248 cm2
Volume = Área da base x altura = 8.6/2 x 10 → V = 240 cm3
2. Uma barra de doce de leite (paralelepípedo
retângulo), com 5 cm x 6 cm x 7 cm, foi completamente envolvida com papel
laminado. Se a barra for cortada em cubos de 1 cm de aresta, quantos cubos
ficarão sem nenhuma cobertura de papel laminado?
Resolução :
Como a barra de dimensões a = 7 cm , b = 6 cm e c = 5
cm, ao ser cortada
em cubos de 1cm de aresta, somente ficará sem nenhuma cobertura de
papel laminado, nos
pedaços internos, que formarão outro
paralelepípedo de dimensões a' = 5 cm, b'
= 4 cm e c' = 3 cm, então
haverão 5 . 4 . 3 = 60 cubinhos de 1 cm3 de volume.
3. A área da superfície da Terra é estimada em
510.000.000 km2. Por outro lado, estima-se que, se todo vapor de
água da atmosfera fosse condensado, o volume de líquido resultante seria de
13.000km3. Imaginando que toda essa água fosse colocada no interior
de um paralelepípedo retângulo, cuja área da base fosse a mesma da superfície
da Terra, qual a medida mais próxima da altura que o nível da água alcançaria ?
Resolução :
Como o Volume de um paralelepípedo = área da base . altura, então
13000 km3 = 510.000.000 km2.H →
H = 13000/510.000.000 = 13/510.000 →
H = 0,0000254 km = 2,54 cm
4. Um tanque tem a forma de um paralelepípedo
retângulo cuja área da base é 0,96 m2. Se os 1152 litros de água em
seu interior ocupam os 2/3 de sua capacidade, então qual a altura desse
tanque, em metros ?
Resolução :
Volume de um paralelepípedo = área da base . altura, então
V = 0,96.H .
Se os 1152 litros(1,152 m3) de água em seu
interior ocupam os 2/3 de sua
capacidade, então 1,152 = 2/3 . V → 1,152 = 2/3 .
0,96H → 1,152 = 0,64H
H = 1,152/0,64 → H = 1,8 m
5. A base de uma caixa retangular tem dimensões 2 cm e
3 cm. Colocam-se 21,6 gramas de um certo líquido nessa caixa. Se cada 0,9 grama
desse líquido ocupa 1 cm3, então qual o nível do líquido na
caixa ?
Resolução :
Volume de um paralelepípedo = área da base . altura, então
V = 2.3.H .
Se cada 0,9 grama desse líquido ocupa 1 cm3,
então 21,6g ocuparão
24 cm3.
Como V = 2.3.H → 24 =
6H → H = 4 cm.
6. Deseja-se construir uma caixa aberta, com o formato
de um cubo. O material utilizado na base, mais resistente, custa R$ 5,00 o
metro quadrado e o material usado nas faces laterais, menos resistente, custa
R$2,00 o metro quadrado . Qual a medida da aresta da caixa de maior volume que
se pode construir por um preço não superior a R$ 72,00?
Resolução :
Considere um cubo de aresta ''a'' metros.
Área da base de um cubo = a2 → ao custo de R$ 5,00 o metro quadrado
Área lateral de um cubo = 4a2 →
ao custo de R$ 2,00 o metro quadrado
Área total de um cubo = 2 . Abase + Alateral = 2a2
. 5 + 4a2 . 2 = 72 →
10a2 + 8a2 = 72 → 18a2 = 72 → a2
= 72/18 → a2 = 4 → a = 2 m
7.
A base de uma pirâmide de 6cm de altura é um quadrado de 8cm de perímetro.
Calcule seu volume.
Resolução :
Como a base é um quadrado de perímetro 8 cm, entao
cada lado da base mede 2 cm.
O Volume da pirâmide é V = 1/3. Áreabase x
altura = 1/3. 22. 6 = 8 cm3
8. Calcule o volume de uma pirâmide de 12cm de altura,
sendo a base um losango cujas diagonais medem 6cm e 10cm.
Resolução :
Como a base é um losango de diagonais 6 cm e 10 cm,
então sua área mede D.d/2
= 6.10/2 = 30 cm2.
O Volume da pirâmide é V = 1/3. Áreabase x
altura = 1/3. 30 . 12 = 120 cm3
9. Um fazendeiro construiu, para guardar sua colheita,
um celeiro cuja forma é a de um sólido, composto de um prisma quadrangular
reto, que tem sobre ele uma pirâmide de igual base e com 3m de altura. Se a
diagonal da base mede 10m e a altura do prisma é 3/5 dessa diagonal, calcule em
litros, a capacidade total desse celeiro.
Resolução :
Se a diagonal da base mede 10m e a altura do prisma é
3/5 dessa
diagonal, então : d = lado. √2 → 10 = l√2 → l = 10/√2 → l = 5√2 m
altura do prisma = 3/5 de diagonal 3/5 de 10 = 6 m
Portanto o volume do sólido é igual a soma do volume
do prisma com o
da pirâmide, ou seja VSolido = VPrisma
+ VPiramide = ABase.HPr + 1/3 . ABase.HPi
→
VSolido = (5√2)2. 6 + 1/3 . (5√2)2.
3 → V = 300 + 50 → V = 350 m3 ou
V = 350.000 litros
10. Um fabricante de goiabada vende seu produto em
latas cilíndricas (raio r e altura h) ao preço de R$2,40 a lata.
Ele pretende substituir a embalagem que usa por outra lata, também
cilíndrica (raio 2r e altura h/2 ). Se o preço de venda de uma lata é
diretamente proporcional ao volume de goiabada no seu interior, por quanto ele
deverá vender a nova lata?
Resolução :
V1 = πr12H1 =
πr2H e V2 = πr22H2
= π(2r)2(H/2) = 2πr2H
Portanto se V1 = πr2H é vendido
por R$ 2,40, então V2 = 2πr2H será
vendido por R$ 4,80
11. Uma panela de forma cilíndrica tem 0,30m de
diâmetro e 0,16m de altura. Pretende-se usar um recipiente com a forma de um
prisma regular quadrangular, com 5 cm de aresta da base e 8 cm de altura, para
levar água à panela. Quantas vezes, no mínimo, esse prisma será usado até que a
panela fique cheia de água?
Resolução :
0,30m de diâmetro e 0,16m de altura 5 cm de aresta da base
(30 cm e 16
cm) e 8 cm de altura
V1 = πr2H = π(15)2.16
≈ 11304 cm2 e V2 = abc = 5.5.8 = 200
cm2
Portanto V1
/ V2 = 11304/200 ≈ 56,52 → 57 vezes
12. A hipotenusa de um triângulo retângulo mede 2 e um
de seus ângulos agudos mede 60° . Girando-se o triângulo em torno do cateto
menor, obtém-se um cone. Qual é o volume desse cone?
Resolução :
Observando o triângulo retângulo : cos 600 = h/2 = 1/2 → h = 1 e
sen 600 = r/2 = √3/2 → r = √3
Volume do cone = 1/3 . π .r2. h = 1/3 . π .(√3)2.
1 → V = π
13. Um cone circular reto, de geratriz medindo 13 cm,
está inscrito em um cilindro circular reto, cujo raio da base mede 5 cm. Qual é
a razão (quociente) entre o volume do cilindro e o volume do cone?
Resolução :
VolumeCilindro / VolumeCone = πr2h/(1/3πr2h)
= 3
14. Considerando a Terra uma esfera cujo diâmetro é
12.800 Km e considerando a Lua uma esfera cujo diâmetro é 1/4 do da Terra, calcule
a razão entre os volumes dos dois astros.
Resolução :
Raio da Lua = 1/4 . Raio daTerra → RT = 4RL
Volume da Terra / Volume da Lua = 4/3 .π.RT3
/ 4/3 .π.RL3 = (RT/RL)3
=
(4RL/RL)3 = 43
= 64 ou o inverso 1/64 pois não foi indicado a ordem.
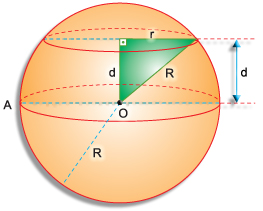
15. Um plano seleciona uma esfera de 34 cm de
diâmetro. Determine o raio da seção obtida, sendo 8 cm a distância do plano ao
centro da esfera.
Resolução :
Como o diâmetro da esfera mede 34 cm, então R = 17 cm.
Portanto R2 = r2 + d2 → 172 = r2
+ 82 → r2 = 289 – 64 → r2 = 225 → r = 15 cm
16. Determine a área de uma superfície esférica, sendo
26π cm o comprimento da circunferência do círculo máximo.
Resolução :
Como o comprimento da circunferência do círculo máximo
é 26π cm,
então 2πR = 26π → R = 13 cm.
Portanto a área de uma superfície esférica mede 4πR2
= 4π(13)2 =
676π cm2
17. Determine a área da superfície e o volume de uma
esfera, sabendo que o seu raio mede 1/5 do raio de outra esfera cujo volume é
4.500π cm3.
Resolução :
Se V = 4/3 .π.R3 = 4500π → 4/3R3
= 4500 → R3 = 4500.3/4 → R = 3√3375 →
R = 15 cm.
A área da superfície e o volume de uma esfera, sabendo
que o seu raio
mede 1/5 do raio de outra esfera apresentada, r = 1/5
de R = 3 cm.
Área = 4πr2 = 4π32 = 36π cm2 e V = 4/3 . π.r3 = 4/3 . π.(3)3
= 36π cm3
Nenhum comentário:
Postar um comentário