1. Dados
fornecidos ao setor responsável pelo controle de saúde infantil, em determinada
escola, indicam que 32 crianças já tiveram caxumba, 25 tiveram catapora e 37,
rubéola.
Sabendo-se que 12 crianças tiveram exatamente duas dessas
doenças e que 4 já tiveram todas, é correto concluir que o número de crianças
que já teve, pelo menos, uma delas está no intervalo :
01) [50, 56]
02) [57, 63]
03) [64, 69]
04) [70, 76]
05)
[77, 83]
Vejamos
:
Observando o
diagrama, podemos notar que :
● 32 crianças tiveram caxumba → x + a + b + 4 = 32 → x + a + b = 28 (eq. I)
● 25 tiveram catapora → y + b + c + 4 = 25 → y + b + c = 21 (eq. II)
● 37, rubéola → z + a + c + 4 = 37 → z + a + c = 33 (eq. III)
● 12
crianças tiveram exatamente duas dessas doenças → a + b + c = 12
Somando as equações I , II e III, obtemos :
x + y + z + 2.(a + b + c) = 28 + 21 + 33 → x + y + z + 2.12 = 28
+ 21 + 33 →
x + y + z + 24 = 82 → x + y + z
= 82 – 24 → x + y + z = 58
● o
número de crianças que já teve, pelo menos, uma das doenças →
x + y + z + a + b + c + 4 = 58 + 12 + 4 = 74
2. Em uma
Comunidade de Cuiabá, durante uma campanha de vacinação, que durou N dias,
foram vacinadas 2142 crianças. Sabendo-se que a média diária de crianças
vacinadas é um número inteiro, que no dia mais movimentado foram vacinadas 91
crianças, e, no menos movimentado, 56 crianças, é correto afirmar que o valor
de N é :
01) 34
02) 48
03) 56
04) 63
05) 72
Vejam :
Sabendo que o número de crianças vacinadas é "inteiro"
e através das alternativas abaixo podemos notar que,
● 2142 crianças : 34
dias = 63 crianças por dia
● 2142 crianças: 48 dias = 44,625 crianças por dia (não convém)
● 2142 crianças: 56 dias = 38,25 crianças por dia (não convém)
● 2142 crianças: 63
dias = 34 crianças por dia
● 2142 crianças: 72 dias = 29,75 crianças por dia (não convém)
Como no dia de menor movimento tiveram 56 crianças e no de
maior movimento, 91crianças, então a única alternativa correta
é N =
34 dias, cujo número de crianças é 63.
3. Admitindo-se os dados recolhidos em laboratórios de Cuiabá,
da
análise desse gráfico, pode-se concluir:
01) A maior despesa de um paciente é de R$ 2056,00.
02) Existem 20 pacientes com despesas superiores a R$ 900,00.
03) Existem, apenas, 11 pacientes com despesas inferiores a R$ 900,00.
04) Apenas um terço do total de pacientes tem despesas
inferiores a
R$ 1000,00.
05) A receita total dos laboratórios, por esses pacientes,
corresponde a R$ 33200,00.
Vejamos :
01) FALSO, a maior despesa de um paciente é de R$ 1750,00.
02) FALSO, existem 18 pacientes com despesas superiores a R$ 900,00.
03) FALSO, existem, apenas, 14 pacientes com despesas inferiores a R$ 900,00.
04) FALSO, apenas um terço(?) do total de pacientes(32) tem
despesas inferiores a R$ 1000,00(14)
05) VERDADEIRO, a receita total dos laboratórios, por esses pacientes,
corresponde a R$ 33200,00.
Receita
= 4x1700 + 6x800 + 8x600 + 14x1200 = 6800 + 4800 + 4800 + 16800 = R$ 33200,00.
4. Após um paciente, com uma febre de 40,2°C, ser medicado, sua
temperatura diminuiu a uma taxa constante de 0,1°C a cada 5min.
Se m(T) = aT + b, em que a e b são constantes, é a função que
descreve quantos minutos se passaram, a partir da medicação, até a temperatura
chegar ao valor T, então o valor de a é igual a :
01) − 50
02) − 25
03) 0,02
04) 25
05) 50
Vejamos :
Segundo a
situação apresentada,
40,2 →
40,1 → 40
→ 39,9 →
39,8 → 39,7
→ 39,6 =
...
0 5 10 15 20
25 30 .....
Seja F(T) = aT + b, a
função que descreve, então,
(0; 40,20)
→ 40,2 = a.0 + b → 40,2 = b
(5, 40,10) →
40,1 = a.5 + b → 40,1 = 5a + 40,2
Resolvendo o
sistema, obtemos 5a = - 0,1 → a = -1/50 → F(T) = -1/50 .T + 40,2
Fazendo F(T) = -1/50 .T +
40,2, como y = (-1/50).x + 40,2 então sua inversa
será x =
(-1/50).y + 40,2 → 50x = - y + 2010 → y = - 50x + 2010 → a = - 50
5. Substância Concentração em mol/litros
I 16.10-4
II 27.10-4
III 12.10-4
A acidez de uma substância é medida pelo valor de seu pH, o qual
é definido como o logaritmo decimal do inverso da concentração de íons de
hidrogênio medido em moles por litro (mol/l).
Na tabela, estão indicadas as concentrações de três substâncias.
Indicando-se por A, B e C o pH de I, II e III e considerando-se
log 2 = 0, 30 e log 3 = 0,47, pode-se afirmar que :
01) A < B < C
02) A < C < B
03) B < A < C
04) B < C < A
05) C < A < B
Vejamos :
A acidez de uma substância é medida pelo valor de seu pH, o qual
é
definido como o logaritmo decimal do inverso da concentração de
íons de
hidrogênio medido em moles por litro (mol/l), ou seja PH = log
1/(H+)
● Substância I → PH = log 1/(H+) → A = log 1/16.10-4
→
A = log 1 – [log 16 + (-4).log 10] → A = 0 - (4 log 2 - 4) = -
4.0,30 + 4 = 2,8
● Substância II → PH = log 1/(H+) → B = log 1/27.10-4
→
B = log 1 – [log 27 + (-4).log 10] → B = 0 - (3 log 3 - 4) = -
4.0,47 + 4 = 2,12
● Substância III → PH = log 1/(H+) → C = log 1/12.10-4
→
C = log 1 – [log 12 + (-4).log 10] → C = 0 - (2 log 2 + log 3 -
4) =
- 2.0,30 – 0,47 + 4 = 2,93. Portanto
B < A < C
6. Atualmente, a rede pública de saúde de um município realiza
180 cirurgias por ano, a um custo médio de R$8000,00 por cirurgia. Investimentos
em medicina preventiva devem reduzir gradualmente o número anual de cirurgias,
em 3 unidades, a cada ano. Por outro lado, a adoção de novas tecnologias deve
elevar o custo médio por cirurgia em R$400,00, a cada ano. O gasto anual do
município com cirurgias deve atingir um máximo igual a :
01) R$1.640.000,00
02) R$1.710.000,00
03) R$1.860.000,00
04) R$1.920.000,00
05) R$2.060.000,00
Vejamos :
● A rede pública de saúde realiza 180 cirurgias por ano, a um
custo médio de R$8000,00 por cirurgia → Custo anual = 180 x 8000 = R$
1.440.000,00.
● Investimentos devem reduzir o número anual de cirurgias, em 3
unidades, a cada ano. Por outro lado, a adoção de novas tecnologias deve elevar
o custo médio por cirurgia em R$400,00, a cada ano →
Custo anual = (180 - 3).(8000 + 400) = R$ 1.486.800,00.
● Portanto de uma maneira geral o custo anual deverá
apresentar o seguinte comportamento,
Custo anual = (180 – 3x).(8000 + 400x), onde "x" é dado em anos.
Portanto C(x) = 3(60 – x).400(20 + x) →
C(x) = 1200(60 – x).(20 + x) → C(x) = 1200(1200 + 60x – 20x – x2)
→
C(x) = 1200(- x2 + 40x + 1200) → C(x) = - 1200 x2
+ 48000x + 1440000
● O gasto anual do município com cirurgias deve atingir um
máximo igual
ao yVértice = - ∆/4a = - (b2 – 4.ac)/4a =
- (480002 – 4.(-1200).1440000)/4(- 1200)
= - (2304000000 + 6912000000)/(- 4800) = = - (23040000 +
6912000)/(- 48) =
= 92160000/48 = R$ 1.920.000,00.
7. Considerando-se P(x) um polinômio do quarto grau, com
coeficientes reais, é correto concluir que P(x) pode ter como raízes os números
:
01) – 3, – 2i, – 1, 0.
02) – 3i, – 2, 0, 3i.
03) – 2, –Ö3 , i, 1.
04) – 1, i,Ö3 , 3i.
05) – 2i, – 1, 0,Ö2i.
Vejamos :
Como P(x) um polinômio do quarto grau, com coeficientes reais,
então
apresenta 4 raízes.
Levando em consideração que as raízes complexas veem sempre aos
pares, ela e seu conjugado, então a única alternativa correta é a 02.
8. Os segmentos PQ e ML, na figura, representam um prédio e um
poste, respectivamente, situados em lados opostos de uma rua, de tal modo que
do ponto P, na base do prédio, se visualiza uma lâmpada L colocada
no topo do poste, segundo um ângulo de 15º com a horizontal e do
ponto Q, no topo do prédio, se visualiza o ponto L, segundo um ângulo de 30º
com o prédio. Desprezando-se as alturas dos observadores e sabendo-se que sen215o
= (2 - Ö3)/4, pode-se concluir que a altura do poste é, aproximadamente,
igual a :
01) 2,8m
02) 3,6m
03) 4,0m
04) 4,5m
05) 5,6 m
Vejamos :
Observando o ∆QPL notamos que como os ângulos QPL e QLP
apresentam a mesma medida, 750, então QL mede 30 m.
Observando o ∆QL'L notamos que é retângulo, com hipotenusa 30 m
e
cateto QL' = 30 – h, então cos 300 = (30 - h)/30 → Ö3/2 = (30 - h)/30 →
30Ö3/2 = 30 - h → 15Ö3 = 30 - h → h = 30 - 15Ö3 → h = 30 – 25,5 → h = 4,5
m
9. Considerando-se M (2x2) tal que m11 = 1 ; m12
= x ; m21 = x e m22 = 1 uma matriz real, é correto
afirmar que o conjunto-solução da inequação
[det (M2 - M)]
< 3x2 é o intervalo :
01) (- ¥, - 4]
02) (- 4, - 2]
03) (- 2, 2)
04) [2, 4]
05) (4, + ¥)
Vejamos :
Como det (M2 - M) `< 3x2 , então x2.x2
– x.x < 3x2 → x4 – x2 < 3x2 →
x4 – 4x2 < 0 → x2(x2
– 4) < 0 → x2 > 0 e (x2 – 4) < 0 → x2 >
0, sempre e
x2 – 4 < 0
----- -2 ---- 2 ---- - 2 < x < 2
10. Em uma comunidade, o número aproximado de pessoas que toma
conhecimento de determinado fato, t meses após ele ter ocorrido, pode ser
estimado através do modelo matemático definido pela função
f(x) = 1800/(3 + 5.2-t). A partir dessa expressão,
considerando-se log 2 = 0,30 e log 3 = 0,48, para que 375 pessoas tomem
conhecimento de um fato, após a sua ocorrência, estima-se que o número de dias
necessários é igual a :
01) 36
02) 44
03) 52
04) 60
05) 72
Vejamos :
Como o modelo matemático foi definido pela função f(x) = 1800/(3
+ 5.2-t),
então para 375 pessoas, vem 375 = 1800/(3 + 5.2-t) → 3
+ 5.2-t = 1800/375 →
3 + 5.2-t = 24/5 → 15 + 25.2-t = 24 → 25.2-t
= 24 - 15 → 25.2-t = 9 → 2-t = 9/25
log 2-t = log 9/25 → - t . log 2 = log 9 – log 25 → -
t . log 2 = 2 log 3 – 2 log 5
- t . 0,30 = 2 . 0,48 – 2 log 10/2 → - 0,30t = 0,96 – 2(log 10 –
log2) →
- 0,30t = 0,96 – 2(1 – 0,30) → - 0,30t = 0,96 – 1,4 → - 0,30t =
– 0,44 →
30t = 44 → t = 44/30 meses → t = 44/30 . 30 = 44 dias.
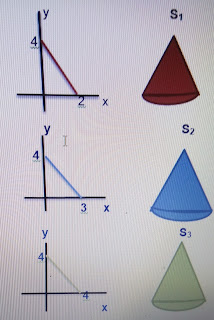
11. As retas de equações r1: y + 2x - 4 = 0, r2:
3y + 4x - 12 = 0 e r3: y + x - 4 = 0 determinam com os eixos
coordenados regiões triangulares, respectivamente, R1, R2 e
R3, contidas no 1º quadrante do plano xOy.
Girando-se R1, R2 e R3, 360º em
torno do eixo Oy, obtêm-se sólidos S1, S2 e S3,
cujos volumes V1, V2 e V3
01) são iguais.
02) são tais que V1 = 4 V2 - 2 V3.
03) são tais que V1/2 = V2/3 = V3/4
04) formam uma progressão aritmética.
05) formam uma progressão geométrica.
Vejam :
r1: y + 2x - 4 = 0 → y = - 2x + 4
r2: 3y + 4x - 12 = 0 → y = -4x/3 + 4
r3: y + x - 4 = 0 → y = - x + 4
V1 = πr2h/3 = π22.4/3 = 16π/3
V2 = πr2h/3 = π32.4/3 = 12π
V3 = πr2h/3 = π42.4/3 = 64π/3
Portanto
V1 = 4 V2 - 2 V3 → V1 = 4.12π – 2.64π/3
→ V1 = 48π – 128π/3 →
V1
= (144π – 128π)/3 → V1 = 16π/3
12. Considere um trapézio isósceles de área S = 28cm2,
lados paralelos medindo 4cm e 10cm, respectivamente, e P, um ponto qualquer
interior ao trapézio. Se n cm é a soma das distâncias de P aos quatro vértices
desse quadrilátero, então o menor valor inteiro de n é :
01) 7
02) 9 QUESTÃO INCOERENTE
03) 10
04) 11
05) 13
Vejamos :
Note que esse valor de "n" poderá variar a depender da
posição do ponto P, acarretando numa questão incoerente.
Vamos imaginar, como exemplo, que o ponto P esteja localizado no
ponto médio de sua base média, conforme a figura.
Como a área é igual a 28, então S = (b + B).h/2 → (4 + 10).h/2 =
28 →
7h = 28 → h = 4 cm.
Segundo o ∆AQP → AP2 = AQ2 + QP2
→ AP2 = 22 + 22 → AP = 2Ö2cm = BP
Segundo o ∆MDP → PD2 = PM2 + MD2
→ PD2 = 22 + 52 → PD = Ö29cm = PC
Se n cm é a soma das distâncias de P aos quatro vértices desse
quadrilátero → n = AP + BP + CP + DP → n = 2Ö2 + 2Ö2 + Ö29 + Ö29 →
n = 4Ö2 + 2Ö29 → n » 5,65 + 10,77 → n » 16,42 cm
13. Os pontos A = (− 4, 0), B = (0, 2) e C são vértices de um
triângulo.
A área do maior triângulo que se pode obter, considerando C um
ponto da circunferência de centro na origem e raio r = Ö5 u.c., é igual, em u.a., a :
01) 9
02) 10
03) 11
04) 12
05) 13
Vejamos :
Observando as condições apresentadas, notamos que para a área do
∆ABC seja máxima é necessário que a altura em relação à base AB,
seja
também máxima.
Como as retas r e s são paralelas então as = ar
= (yB - yA)/(xB - xA) =
= (2 - 0)/(0 - (-4)) → as
= ar = 1/2 → "s": y = x/2 + b.
Portanto o ponto C deverá ser obtido através da interseção
das equações no sistema "x2 + y2 = 5 Ç y = x/2 + b" . Como
a reta é
tangente à circunferência, então o discriminante será nulo, ou
seja
x2 + (x/2 + b)2 = 5 → x2 + x2/4
+ xb + b2 = 5 → 5x2/4 + xb + b2 = 5 →
5x2 + 4bx + 4b2 – 20 = 0 → ∆ = (4b)2
– 4.(5).( 4b2 – 20) = 16b2
– 80b2 + 400
∆ = - 64b2 + 400 = 0 → - 64b2 = - 400 → 4b2
= 25 → b2 = ± 25/4 → b = ± 5/2 →
Se a reta "s" intercepta o eixo y abaixo da origem,
então b = - 5/2 e
"s" apresentará a equação y = x/2 - 5/2.
Resolvendo o sistema "x2 + y2 = 5 Ç y = x/2 - 5/2" → x2
+ (x/2 - 5/2)2 = 5 →
x2 + x2/4 – 2 . x/2 . 5/2 + 25/4 = 5 → 4x2
+ x2 – 10x + 25 = 20 →
5x2 – 10x + 5 = 0 → x2 – 2x + 1 = 0 → xC
= 1 e yC = - 2 → C(1, -2)
Finalmente a área do ∆ ABC poderá ser obtida através do valor
absoluto
do dispositivo prático :
A∆ABC = ½ . (
-4 . 2 + 0 . (-2) + 1 . 0 - (-4) . (-2) – 1 .2 – 0 .0 )
A∆ABC
= ½ . ( - 8 – 8 – 2 ) = 9 u.a., em valor
absoluto








Nenhum comentário:
Postar um comentário