1.Em um estudo feito por uma empresa de mercado, no Brasil,
registra-se que 67% dos consumidores brasileiros não compraram produto algum,
via internet, nos últimos 12 meses. Além disso, nesse estudo, afirma-se que 9%
dos consumidores brasileiros adquiriram somente um item, via internet, no mesmo
período.
Disponível em: http://goo.gl/tPWAtl. Acesso em: jul. 2014 (Adaptado)
Em relação ao total de consumidores brasileiros que comprou
algum produto via internet nos últimos 12 meses, é CORRETO afirmar que, aproximadamente,
A) 3% adquiriram somente um item nesse período.
B) 9% adquiriram somente um item nesse período.
C) 13% adquiriram somente um item nesse período.
D) 27% adquiriram somente um item nesse período.
Vejamos :
Registra-se que 67% dos consumidores brasileiros não compraram
produto algum,
então 100% - 67% = 33% compraram algo.
Além disso, afirma-se que 9% adquiriram somente um item.
Em relação ao total de consumidores brasileiros que comprou
algum produto via i
internet, é correto afirmar → Se 33% → 100%, então 9% → x,
x = 100.9/33 → x =
27%
2. Considere as sentenças a seguir:
I. 5-1/3 = 3Ö(1/5) II. 3.22/9 = 62/9 III.
(4/9)-3/2 = 27/8
É CORRETO afirmar
que são VERDADEIRAS :
A) apenas as sentenças I
e II.
B) apenas as sentenças I
e III.
C) apenas as sentenças II
e III.
D) todas as sentenças.
Vejamos :
I)
VERDADEIRA, 5-1/3 = 3Ö(1/5).
II)
FALSA, 3.22/9 ǂ 62/9
III)
VERDADEIRA, (4/9)-3/2 = (9/4)3/2
= [(3/2)2]3/2 = (3/2)3 = 3Ö(3/2)4 = 27/8
3. A figura a seguir apresenta o hexágono ABCDEF desenhado em uma malha
quadriculada cujas dimensões são 5 cm x 5 cm.
Com base nessas informações, é CORRETO afirmar que a área,
em cm2, do hexágono ABCDEF,
é :
A) 5.
B) 6.
C) 7.
D) 8.
Vejamos :
Podemos determinar a área do hexágono ABCDEF através da soma das
áreas AFB, FBDE e BCD.
ABCDEF = AFB + FBDE + BCD
= 2.2/2 + (2 + 1).2/2 + 2.1/2 = 2 + 3 + 1 = 6
4. Marta quer saber quanto pesam, juntos, os objetos X, Y e Z.
Porém, não é possível apoiá-los na balança disponibilizada. Além disso, Marta
não consegue carregar os três objetos simultaneamente.
Dessa forma, inicialmente, ela sobe na balança carregando os
objetos X e Y. A balança registra 70kg.
Em seguida, desce e sobe novamente, carregando, dessa vez,
apenas o objeto Z. A balança registra então o total de 73 kg.
Sabendo que o peso de Marta, individualmente, é 62 kg, determine
a soma dos pesos dos objetos X, Y e Z.
A) 8.
B) 11.
C) 16.
D) 19.
Vejamos :
Se Marta + X + Y = 70 kg,
Marta + Z = 73 kg e Marta = 62 kg, então
62 + X + Y = 70 → X
+ Y = 8 kg,
62 + Z = 73 → Z = 11 kg.
A soma dos pesos dos objetos X, Y e Z é 19 kg.
5. A tabela a seguir mostra os cinco países que mais compraram
ingressos na Copa do Mundo de 2014.
Disponível em: http://goo.gl/Dd8J2a. Acesso em: jul. de 2014 (Adaptado).
De acordo com os dados da tabela, assinale a alternativa INCORRETA.
A) A quantidade de ingressos que a Argentina comprou aproximadamente
4% da quantidade de ingressos comprada pelo Brasil.
B) A quantidade de ingressos que o Brasil comprou é aproximadamente
400% maior que a soma da quantidade de ingressos comprados pelos outros países.
C) O total de ingressos comprado por Alemanha, Argentina e Inglaterra
é 90% da quantidade de ingressos comprada pelos EUA.
D) O total de ingressos comprado pela Argentina e pela
Inglaterra é 60% da quantidade de ingressos comprada pelos EUA.
Vejamos :
A) CORRETA, a quantidade de ingressos que a Argentina comprou
aproximadamente 4% da quantidade de ingressos comprada pelo Brasil → 60000/1600000
= 0,0375 = 3,75%
B) INCORRETA, a quantidade de ingressos que o Brasil comprou é
aproximadamente 400% maior que a soma da quantidade de ingressos comprados
pelos outros países → 1600000/380000 = 160/38 = 4,21 = 1 + 3,21 = 100% + 321%
C) CORRETA, o total de ingressos comprado por Alemanha, Argentina e
Inglaterra é 90% da quantidade de ingressos comprada pelos EUA → 180000
= 90% de 200000
D) CORRETA, o total de ingressos
comprado pela Argentina e pela Inglaterra é 60% da quantidade de ingressos comprada
pelos EUA → 120000 = 60% de 200000
6. No primeiro dia de aula após as férias, a professora perguntou
aos alunos para onde eles tinham viajado. A professora organizou as respostas
dos alunos em: fazenda, montanha e praia. Posteriormente, apresentou o seguinte
diagrama:
Com base nessas informações, é CORRETO afirmar que a região hachurada representa todos os alunos
que viajaram para a :
A) fazenda e para a praia.
B) montanha e para a praia.
C) montanha e para a praia, mas não para a fazenda.
D) fazenda e para a praia, mas não para a montanha.
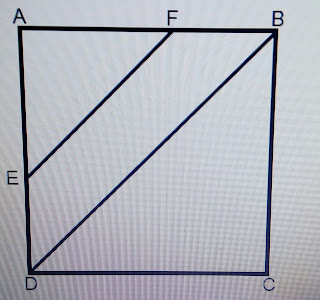
7. A figura, a seguir, apresenta um quadrado de vértices A, B, C e D, cujo lado mede 5 m. O trapézio isósceles
de vértices E, F, B e D, de bases EF e DB, possui área igual a 4,5 m2.
Com base nessas informações, é CORRETO afirmar que o perímetro, em metros, do trapézio EFBD, é :
A) Ö2 + 18.
B) 5Ö2 - 9.
C) 9Ö2 + 1.
D) 9Ö2 + 2.
Vejamos :
Como o lado do quadrado ABCD mede 5 m, então sua área mede 25 m2
e sua diagonal BD pode ser obtida através da relação d = l√2→BD = 5√2 m
Agora, observando a figura seguinte,
Área AEF/ Área ABD = (EF/BD)2 → (25/2 – 4,5)/(25/2) =
(EF/5√2)2 →
8/(25/2) = (EF/5√2)2 → 16/25 = (EF)2/50 →
(EF)2 = 32 → EF = √32 →
EF =
4√2 m.
Ainda na mesma figura,
EF/(AB - FB) = DB/AB → 4√2/(5 - FB) = 5√2/5 → 4√2/(5 - FB) = √2
→
4 = 5 - FB → FB =
1 m e DE = 1 m.
Finalmente o perímetro do trapézio EFBD é igual a EF + FB + BD +
DE =
4√2 + 1 + 5√2 + 1 = (9√2
+ 2) m
8. Seja M = (a2 – 2ab + b2)(a2
– b2)/(a2b + ab2) em que a e b
em que a e b são números reais, tais que a ǂ 0, b ǂ 0 e a ǂ - b.
Determine a alternativa que mostra uma forma simplificada de M.
A) M = (a – b)3/ab
B) M = 2(a – b)/b(a + b)
C) M = (a – b)4/ab(a + b)
D) M = -2ab(a2 – b2)/(b + a)
Vejamos :
Seja M = (a2 – 2ab + b2)(a2 – b2)/(a2b
+ ab2) = (a – b)2.(a – b)(a + b)/ab(a + b)=
= (a – b)2.(a – b)/ab = (a – b)3/ab
9. De acordo com o levantamento da ferramenta de inteligência em
marketing digital da Serasa Experian, o Facebook é o líder isolado nos
acessos às redes sociais no Brasil.
Observe a seguir alguns resultados aproximados sobre esses
acessos.
1.
Facebook: 70%
2.
YouTube: 18%
3. Ask.fm:
2%
4. T
witter: 2%
5. Orkut:
1,5%
6. Outras:
6,5%
Disponível em:
http://goo.gl/U5XRyI.Acesso em: jul. de 2014 (Adaptado)
O gráfico de setor, referente a essas informações, seria formado
por seis setores. Qual seria a diferença aproximada, em graus, dos ângulos dos
setores referentes ao Facebook e ao YouTube, respectivamente?
A) 52º.
B) 94º.
C) 187º.
D) 252º.
Vejamos :
Como Facebook: 70% e YouTube: 18%, então Facebook – YouTube =
52%.
Se 100% → 3600, então 52% → x. Portanto x = (52% .
3600)/100% = 187,20
10. Considere os conjuntos I, J e K:
I= {a pertence ao conjunto dos número
reais / a < 8}
J= {b pertence ao conjunto dos
números racionais / b > 3}
K= {c pertence ao conjunto dos número
inteiros / -2 ≤ c ≤ 5}
Assinale a alternativa VERDADEIRA.
A) O maior elemento do conjunto I é o número 7.
B) O menor elemento do conjunto J é o número 3,1.
C) A união dos conjuntos I
e J é o conjunto dos
números reais.
D) A interseção dos conjuntos J e K possui apenas
dois elementos.
Vejamos :
A) FALSA, o maior elemento do conjunto I não
é o número 7, pois o universo são os números reais.
B) FALSA, o menor elemento do conjunto J não é o
número 3,1, pois o universo são os
números racionais.
C) FALSA, a união dos conjuntos I e J não é o
conjunto dos números reais, pois o
universo de J são os números racionais.
D) VERDADEIRA, interseção dos
conjuntos J e K possui apenas dois elementos, b >
3 e
-2 ≤ c ≤ 5 → 3 < b ≤ 5, no
universo dos números inteiros, {4, 5}
11.A figura a seguir representa uma plantação que ocupa um
terreno retangular delimitado por uma cerca de arame. Também está representado
nessa figura que, em um ponto do terreno, a 3 metros
de uma das laterais da cerca, há um irrigador de água. A água
desse irrigador cobre uma superfície circular de raio igual a 6 metros. Se a
região hachurada na figura representa a superfície abrangida pela água desse
irrigador, no terreno ocupado pela plantação, determine a área, em m2, dessa
superfície.
A) 9 + 6π.
B) 18 + 6π.
C) 9Ö3 +24π.
D) 18Ö3 +24π.
Vejamos :
Observando o triângulo cos α = 3/6 → cos α = 1/2 → α = 600
Portanto a área irrigada poderá ser de obtida através da
diferença entre a
área do círculo e a do segmento circular de 1200 →
A = πr2 - (απr2/3600 - 1/2 . r2.sen
α) = π62 - (1202 π62/3600 - 1/2 . 62.sen
1200)
A = 36π - (36π/3 - 1/2 . 36. √3/2) → A = 36π - (12π - 9√3) → A = 24π + 9√3
12. O primeiro colocado do Campeonato Brasileiro de 2013 recebeu
9 milhões de reais pela conquista da posição. O segundo, o terceiro e o quarto
colocados receberam, respectivamente, 6 milhões, 4 milhões e 3 milhões de
reais.
Disponível em: <http://migre.me/kAo6j> . Acesso em: 22 jun. 2014
(Adaptado).
Seja S a soma dos
montantes distribuídos entre esses quatro primeiros colocados. Supondo que S tivesse sido dividida entre o
primeiro, o segundo, o terceiro e o quarto colocado, em partes inversamente
proporcionais a 1, 2, 3 e 4, respectivamente, é CORRETO afirmar que :
A) o primeiro colocado receberia R$1. 560. 000,00 a menos do que
recebeu.
B) o segundo colocado receberia R$ 600. 000,00 a mais do que
recebeu.
C) o terceiro colocado receberia R$ 380. 000,00 a mais do que
recebeu.
D) o quarto colocado receberia R$ 360. 000,00 a menos do que
recebeu.
Vejamos :
10 Colocado = X = 9 milhões, 20 Colocado = Y = 6 milhões
30 Colocado = Z = 4 milhões, 40 Colocado = W = 3 milhões
S = 9 + 6 + 4 + 3 = 22 milhões, em partes inversamente a 1, 2, 3
e 4
X/(1/1) = Y/(1/2) = Z/(1/3) = W/(1/4) = 22/(1/1 + 1/2 + 1/3 +
1/4)
X = 2Y = 3Z = 4W = 22/[(12 + 6 + 4 + 3)/12] = 22.12/25 = 10,56
X = 10,56 milhões = R$ 10.560.000,00;
Y = 5,28 milhões = R$ 5.280.000,00;
Z = 3,52 milhões = R$ 3.520.000,00 e
W = 2,64 milhões = R$
2.640.000,00.
O quarto colocado
receberia R$ 360. 000,00 a menos do que recebeu →
R$ 2.640.000,00 + R$ 360.000,00
= R$ 3.000.000,00.
13. Na figura a seguir, o ponto P representa um posto de combustível situado na Estrada r (retilínea).
Além disso, o ponto P está
equidistante dos pontos A e B, que representam os centros das
cidades Alegria e Beleza, respectivamente (AP = BP). Para melhorar o acesso dos moradores das cidades
A e B ao posto, serão construídas duas estradas
retilíneas, perpendiculares entre si, que ligam A ao P e B ao P.
As distâncias dos centros das cidades Alegria e Beleza à Estrada r são,
respectivamente, 10 km e 7 km.
Determine
o comprimento aproximado, em
quilômetros, da estrada retilínea que ligará o centro de Alegria (A) ao posto
(P).
A) 10.
B) 12.
C) 14.
D) 17.
Vejamos :
Observando a figura acima e através de semelhança de triângulos,
10/z = y/7 → yz = 70 → y
= 70/z
Agora através do teorema de Pitágoras,
x2 = 102 + y2 e x2
= 72 + z2 →
102 + y2 = 72 + z2 → 100 + y2
= 49 + z2 →
z2
– y2 = 51 → z2 – (70/z)2
= 51 → z2 – 4900/z2 = 51 → z4 – 4900 = 51z2
→
z4 – 51z2 - 4900 = 0 → fazendo z2
= a, vem a2 – 51a - 4900 = 0 →
∆ = (51)2 – 4.1.(- 4900) = 2601 + 19600 = 22201 → a =
(51 ± 149)/2 → a =
100
Como z2 = a, então z2 = 100 → z = 10 km.
Consequentemente, como
x2 = 72 + z2 → x2 = 72 + 102 → x2 = 149 →
x = √149 → x ≈
12,2 km
14. Três sócios de uma empresa pagaram uma dívida durante 3 meses
seguidos. No primeiro mês, os três juntos pagaram 3/8 do total da dívida. No segundo
mês, os três juntos pagaram 2/5 do restante da dívida.
Sabendo que, no último mês, cada sócio pagou a mesma quantia, qual
a fração do total da dívida cada um deles pagou apenas nesse terceiro mês?
A) 1/8
B) 3/8
C) 9/40
D) 19/40
Vejamos :
Três sócios de uma empresa "x, y e z" pagaram uma
dívida "D" durante 3
meses seguidos.
No primeiro mês, os três juntos pagaram 3/8 do total da dívida. →
3D/8.
No segundo mês, os três juntos pagaram 2/5 do restante da dívida
→
2/5 . (1 - 3/8)D = 2/5 . 5D/8 = D/4.
No último mês, cada sócio pagou a mesma quantia, qual a fração
do total
da dívida cada um deles → (D – 3D/8 - D/4) ÷ 3 = (8D – 3D - 2D)/8
÷ 3 =
= 3D/8 ÷ 3 = D/8
15. Um hospital tinha, em 2012, uma equipe de funcionários
composta por médicos e enfermeiros. Nessa equipe, 37,5% dos funcionários eram
médicos. Em 2013, o hospital contratou mais X enfermeiros para a mesma equipe, mas o número de médicos
permaneceu sem alteração. Após a contratação, a quantidade de médicos passou a
ser 20% da quantidade total de funcionários da equipe.
Determine
a razão entre a quantidade
total de enfermeiros após a contratação e a quantidade total de enfermeiros
existentes antes da contratação.
A) 5/12
B) 12/5
C) 3/20
D) 20/3
Vejamos :
● Com o objetivo de facilitar as operações vamos imaginar que a
equipe
seja formada por 1000 pessoas, por exemplo.
● Em 2012, uma equipe composta por "37,5% de 1000" = 375 médicos e
"62,5% de 1000" = 625 enfermeiros.
● Em 2013, o hospital contratou mais X enfermeiros → "625 + X",
mas o número de médicos "375 " permaneceu sem alteração.
Após a contratação, a quantidade de médicos passou a ser 20% da
quantidade total de funcionários da equipe →
375 = 20% de (1000 + X) → 375 = 0,2.(1000 + X) → 375 = 200 + 0,2X
→
175 = 0,2X → X = 875 enfermeiros.
● A razão entre a quantidade total de
enfermeiros após a contratação e a
quantidade antes da contratação → (625 + 875)/625 = 1500/625 = 12/5







Obrigada, ajudou muito. Você poderia fazer a de 2014 por favor ?
ResponderExcluir