1. (Ueg 2018)
Dados dois
conjuntos, A e B, onde A ∩ B = {b, d}, A U B = {a, b, c, d, e} e B – A = {a}. O
conjunto B é igual a :
a) {a}
b) {c, e}
c) {a, b, d}
d) {b, c, d, e}
e) {a, b, c, d, e}
Resposta
da questão 1: [C]
Como
A ∩ B = {b, d} e B – A = {a} então B = {a, b, d}
2. (Ueg 2018)
O número de
anagramas que se pode formar com a palavra ARRANJO é igual a :
a) 21
b) 42
c) 5040
d) 2520
e) 1260
Resposta
da questão 2: [E]
O cálculo será obtido fazendo uma
permutação de 7 elementos com
repetição de dois deles → P72,2
= 7!/2!.2! = 1260
3. (Ueg 2018)
Uma loja faz
uma promoção: ao comprar qualquer produto, o cliente participa de um jogo, o
qual consiste em girar duas roletas. A roleta A contém os valores e a B os
multiplicadores desses valores. Por exemplo, se um cliente tirar $5 na roleta A
e #2 na roleta B, ele ganha R$ 10,00 (5 x 2 = 10). 6
Dessa forma, considerando as roletas das figuras
apresentadas, se um
cliente participar dessa promoção, a probabilidade
de ele ganhar R$ 5,00 ou menos é de :
a) 5/9
b) 4/9
c) 1/2
d) 1/18
e) 1/3
Resposta
da questão 3:[C]
O número de resultados possíveis para
o experimento pode ser obtido da
seguinte forma: 6 . 3 = 18 ou seja,
para cada um dos 6 resultados da
primeira roleta teremos 3
multiplicadores.
Os pares ordenados (x, y) cujo
produto x . y é menor ou igual a 5 são os
seguintes: (2, 0) , (2, 1) , (2, 2) ,
(5, 0) , (5, 1) , (10, 0) , (20, 0) , (50, 0) e
(100, 0) ou seja, 9 produtos que são
menores ou iguais a cinco.
Logo, a probabilidade P pedida será
dada por: P = 9/18 = 1/2.
4. (Ueg 2018)
Dadas a
funções f(x) = - x2 e g(x) = 2x, um dos pontos de intersecção entre
as funções f e g é :
a) (0,
2)
b) (-
2, - 4)
c) (2,
4)
d) (0,
- 2)
e) (-
2, 4)
Resposta
da questão 4:[B]
Para determinar os pontos de
intersecção entre os gráficos de duas
funções devemos resolver um sistema
com as suas leis de formação.
2x = - x2 → x2
+ 2x = 0 → x = 0 → y = 0 ou x = - 2 → y = - 4
Portanto, os pontos em que os
gráficos se intersectam são: (0, 0) ou
(- 2, - 4).
5. (Ueg 2018)
No centro de
uma cidade, há três estacionamentos que cobram da seguinte maneira:
|
Estacionamento A
|
Estacionamento B
|
Estacionamento C
|
|
R$ 5,00 pela primeira hora
R$ 3,00 por cada hora subsequente
|
R$ 4,00 por hora
|
R$ 6,00 pela primeira hora
R$ 2,00 por cada hora subsequente
|
Será mais vantajoso,
financeiramente, parar :
a) no
estacionamento A, desde que o automóvel fique estacionado por quatro
horas.
b) no
estacionamento B, desde que o automóvel fique estacionado por três horas.
c) em
qualquer um, desde que o automóvel fique estacionado por uma hora.
d) em
qualquer um, desde que o automóvel fique estacionado por duas horas.
e) no
estacionamento C, desde que o automóvel fique estacionado por uma hora.
Resposta
da questão 5:[D]
Valor cobrado pelo estacionamento A
para t horas :
yA (t) = 5 + (t - 1).3 → yA
(t) = 3t + 2
Valor cobrado pelo estacionamento B
para t horas :
YB (t) = 4t
Valor cobrado pelo estacionamento C
para t horas :
YC (t) = 6 + (t - 1).2 → yC
(t) = 2t + 4
Como yA(2) = yB(2)
= yC(2) = 8
Logo, todos cobrarão o mesmo valor,
desde que o automóvel fique
estacionado por duas horas.
6. (Ueg 2018)
Deseja-se
construir um reservatório cilíndrico circular reto com 8 metros de diâmetro e
teto no formato de hemisfério. Sabendo-se que a empresa responsável por
construir o teto cobra R$ 300,00 por m2 o valor para construir esse
teto esférico será de :
Use π = 3,1
a) R$ 22.150,00
b) R$ 32.190,00
c) R$ 38.600,00
d) R$ 40.100,00
e) R$ 29.760,00
Resposta da
questão 6: [E]
Calculando a área A do teto do
reservatório, temos:
A = 4.π.R2/2 = 4.π.42/2
= 32.π ≈ 32 . 3,1 ≈ 99,2 m2
Portanto, o valor pedido para a
construção deste teto será:
99,2 . R$ 300,00 = R$ 29.760,00
7. (Ueg 2018)
A tabela a
seguir apresenta a distribuição dos pontos de uma avaliação realizada com 100
alunos.
|
Pontos
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Alunos
|
2
|
5
|
8
|
10
|
15
|
17
|
15
|
12
|
8
|
4
|
4
|
Analisando-se os dados dessa tabela, a média do
número de pontos desses alunos é igual a :
a) 5,0
b) 5,1
c) 5,2
d) 5,4
e) 5,5
Resposta da questão 7: [B]
Med. = (2.0 + 5.1 + 8.2 + 10.3 + 15.4 + 17.5 + 15.6
+ 12.7 + 8.8 + 4.9 +
+ 4.10)/100 = 510/100 = 5,1
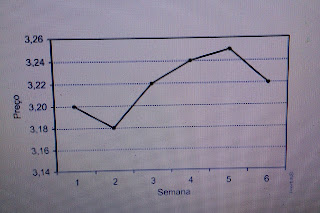
8. (Ueg 2018)
As ações de
uma empresa variaram semanalmente conforme os dados da figura a seguir.
De acordo com
os dados apresentados, o período de maior variação ocorreu entre as semanas :
a) 2
e 3
b) 1
e 2
c) 4
e 5
d) 3
e 4
e) 5
e 6
Resposta da
questão 8:[A]
Variação: considerando que a
distância entre duas linhas horizontais é de
0,02 podemos escrever que as
variações em cada um dos intervalos são:
Entre 1 e 2 : - 0,02
Entre 2 e 3 : + 0,04
Entre 3 e 4: + 0,02
Entre 4 e 5 : menor que 0,02
Entre 5 e 6 : menor que – 0,02 e
maior que – 0,04
Portanto, a maior variação ocorreu
entre as semanas 2 e 3


Muito obrigado por sua ajuda,se todos fossem igual a você o mundo seria melhor.
ResponderExcluirPorque na questão 5 o tempo da função do estacionamento A e C usa o tempo (t-1) em vez de t?
ResponderExcluirdsds
ResponderExcluir