QUESTÕES VESTIBULAR UNIFESP 2018 – TIPO ANALÍTICA - COMENTADAS

1. (Unifesp 2018)  Em uma classe de 16 alunos, todos são fluentes em português. Com relação à fluência em línguas estrangeiras, 2 são fluentes em francês e inglês, 6 são fluentes apenas em inglês e 3 são fluentes apenas em francês.

a) Dessa classe, quantos grupos compostos por 2 alunos podem ser formados sem alunos fluentes em francês?

b) Sorteando ao acaso 2 alunos dessa classe, qual é a probabilidade de que ao menos um deles seja fluente em inglês?

  

De acordo com o enunciado:

                         

a) Calculando: C11,2 = 11!/2!9! = 55 grupos

b) Calculando: P(x) = 1 – C8,2/C16,2 = 1 - 28/120 = 92/120 = 23/30

   

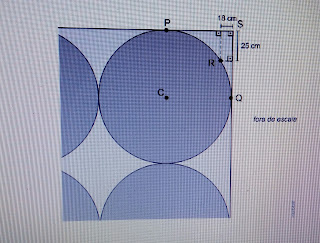
2. (Unifesp 2018)  Em um tapete retangular decorado com círculos idênticos, o círculo de centro C tangencia as laterais do tapete em P e Q O ponto R pertence à circunferência desse círculo e está à distância de 18 cm e de 25 cm das laterais do tapete, como mostra a figura.

                               

a) Calcule a distância de R até o canto superior do tapete, indicado por S. Deixe a resposta indicada com raiz quadrada.

b) Calcule o raio dos círculos que compõem a decoração do tapete.

  

Conforme enunciado:

                            

a) Calculando: RS² = 18² + 25² → RS = √949

b) Calculando: r² = (r - 18)² + (r - 25)² → r² = r² – 36r + 324 + r² – 50r + 625

    r² - 86r + 949 = 0 → r = 13(não convém) ou r = 73

   

3. (Unifesp 2018)  Um estudo médico recrutou 160 pacientes homens com histórico de alterações no antígeno prostático específico (PSA). Os pacientes foram submetidos aos exames laboratoriais de PSA total e de PSA livre e, em seguida, a uma biópsia da próstata. A biópsia apontou, em cada caso, se a patologia era maligna ou benigna. A tabela apresenta os resultados das médias dos exames laboratoriais do grupo de pacientes com patologia maligna e do grupo de pacientes com patologia benigna.

PSA (média)	Biópsia com indicação de patologia maligna	Biópsia com indicação de patologia benigna
PSA total (ng/ml)	10	8
PSA livre (ng/ml)	1,9	2
PSA livre ÷ PSA total	0,19	0,25

Pedro foi um dos pacientes que participou do estudo e seus exames indicaram PSA total = 9,5 ng/ml e PSA livre = 2,28 ng/ml.

a) Calcule o quociente entre o PSA livre e o PSA total de Pedro. Usando esse indicador como referência na comparação com os dados da tabela, indique se o resultado do exame de Pedro está numericamente mais próximo ao resultado médio do exame de quem tem a patologia maligna ou de quem tem a patologia benigna.

b) Sabendo que 40% dos pacientes foram diagnosticados com patologia maligna, calcule a média do PSA total dos 160 pacientes que participaram do estudo.

  

a) Calculando: PSA_total/ PSA_total = 2,28/9,5 = 0,24

 Como 0,24 é mais próximo de 0,25, então Pedro está numericamente mais próximo ao resultado médio do exame de quem tem a patologia maligna ou de quem tem a patologia benigna.

b) Calculando: [10.(160.0,4) + 8.(160.0,6)]/160 = 8,8

4. (Unifesp 2018)  Uma chapa retangular metálica, de área igual a 8,132 m², passa por uma máquina que a transforma, sem nenhuma perda de material, em uma telha ondulada. A figura mostra a telha em perspectiva.

                         

A curva que liga os pontos A e B, na borda da telha, é uma senóide.

Considerando um sistema de coordenadas ortogonais com origem em A, e de forma que as coordenadas de B, em centímetros, sejam (195, 0), a senóide apresentará a seguinte configuração:

  

a) Calcule o comprimento da senóide indicada no gráfico, do ponto A até o ponto B.

b) Determine a expressão da função cujo gráfico no sistema de coordenadas é a senóide de A até B. Determine o domínio, a imagem e o período dessa função.

  

a) Se a chapa possui área igual 8132 m², então o comprimento da senoide

    

    será: Área = 4x → 8132 = 4x → x = 2033 m

b) Calculando: f = 6; T = 195/6; A = 2 e f(x) = A . sen kx

     195/6 = 2π/|k| → k = 4π/65 → f(x) = 2 . sen (4πx/65)

      D(f) = {x ɛ R / 0 ≤ x ≤ 195}  e Im(f) = {y ɛ R / -2 ≤ y ≤ 2} .

5. (Unifesp 2018)  Raquel imprimiu um número x de fotografias ao custo unitário de 54 centavos. Cada foto foi vendida ao preço de 75 centavos sobrando, no final do período de vendas, y fotografias sem vender, o que resultou em um prejuízo de 12 reais em relação ao custo total das impressões.

a) Calcule quantas fotografias foram impressas, para o caso em que y = 100.

b) Determine a expressão de y em função de x para a situação descrita no enunciado.

   Calculando: Custo impressão = 0,54 ; Preço venda = 0,75;

   Fotos vendidas = x – y → 0,75(x - y) – 0,54x = - 12

   a) Calculando: Vendas – Custos = Lucro/Prejuízo

    0,75(x - y) – 0,54x = - 12 → 0,75(x - 100) – 0,54x = - 12 →

    0,75x - 75 – 0,54x = - 12 → 0,21x = 63 → x = 300

    b) Isolando y; 0,75(x - y) – 0,54x = - 12 → 0,75x – 0,75y – 0,54x = - 12 →

     0,21x – 0,75y = - 12 → y = (-0,21x - 12)/-0,75 → y = 0,28x + 16