Professor Luiz Bolinha: QUESTÕES VESTIBULAR Ufu 2017

1. (Ufu 2017) A Secretaria de Saúde de um determinado Estado brasileiro necessita enviar 640 estojos de vacinas para N regiões distintas. Após avaliar as demandas de cada uma dessas regiões a serem atendidas, estabeleceu-se o seguinte esquema de envio:

- para a região 1 serão enviados x estojos;

- para a região 2 serão enviados x estojos;

- para a região 3 serão enviados 2x estojos;

- para a região 4 serão enviados 4x estojos;

e esse padrão se repete nas demais regiões, ou seja, serão enviados tantos estojos a uma região quanto for a soma dos que já foram enviados às regiões anteriores. O valor de x deve ser tal que N é o maior possível e exatamente todos os estojos sejam distribuídos.

Nas condições apresentadas, é igual a N.x

a) 35

b) 30

c) 40

d) 45

Resposta da questão 1:[C]

Do enunciado, temos a sequência: (x, x, 2x, 4x, ... )

Note que a sequência (x, 2x, 4x, ... ) é uma progressão geométrica, onde o

primeiro termo é x e a razão é 2. Observe também que a progressão

geométrica possui (n - 1) termos.

Assim, x + x.(2^{n – 1} - 1)/(2 - 1) = 640 → x + x.2^{n – 1} - x = 640 → x.2^{n – 1} = 640

x.2^{n – 1} = 5.2⁷ → x = 5 e n = 8, pois x e N são naturais e N é o maior

possível. Logo N.x = 8.5 = 40

2. (Ufu 2017) Para realizar uma venda, uma loja virtual solicita de seus clientes o cadastramento de uma senha pessoal que permitirá acompanhar a entrega de sua compra. Essa senha anteriormente era composta por quatro algarismos e uma letra (minúscula), sem quaisquer restrições de posicionamentos entre letra e algarismos. Com o grande aumento no número de vendas, houve a necessidade de ampliação no número de senhas, as quais passaram a ser compostas por cinco algarismos e uma letra (minúscula). Sabe-se que existem 26 letras no alfabeto e 10 algarismos disponíveis.

Se denotarmos por N e M, respectivamente, o número total de senhas possíveis, antes e após a mudança, então, a relação entre N e M é dada por:

a) M = 10N

b) M = 5!N

c) M = 6!N

d) M = 12.N

Resposta da questão 2:[D]

Do enunciado, antes da mudança, temos: _ A _ A _ A _ A _ ,

Onde "A" indica um algarismo qualquer.

Observe que há 5 possibilidades para se colocar a letra minúscula.

Assim, pelo princípio fundamental da contagem, N = 5 . 26 . 10⁴

Analogamente, M = 6 . 26 . 10⁵.

Daí, M/N = 6.26.10⁵/5.26.10⁴ → M/N = 12 → M = 12N

3. (Ufu 2017) Um designer de jogos virtuais está simulando alguns deslocamentos associados com uma pirâmide quadrangular regular, em que o lado do quadrado da base mede 40 cm.

Ele simula a trajetória de um lagarto pelas faces da pirâmide. Inicialmente o lagarto desloca-se de A até E e, posteriormente, de E até F, em que F é o ponto médio de CD. Cada um desses dois trechos da trajetória ocorre em linha reta.

A projeção perpendicular dessa trajetória em ABCD, presente no plano da base da pirâmide, descreve uma curva R, a qual é a união de dois segmentos.

Nessas condições, o comprimento de R, em cm, é igual a :

a) 20√2

b) 40√2

c) 40(1 + √2)

d) 20(1 + √2)

Resposta da questão 3:[D]

Do enunciado e da figura, temos:

G é ponto de encontro das diagonais do quadrado ABCD pois EABCD é uma pirâmide quadrangular regular.

O comprimento de R é dado por AG + GF, pois AG é a projeção perpendicular de AE sobre ABCD e GF é a projeção perpendicular de EF sobre ABCD.

Note que AG = AC/2 e GF = AD/2.

No triângulo ACD, AC² = 40² + 40² → (2AG)² = 2.40² → 4(AG)² = 2.40²

Como AG > 0, √4(AG)² = √2.40² → 2AG = 40√2 → AG = 20√2.

Como AD = 40 cm, GF = 20 cm

Assim, AG + GF = (20√2 + 20) cm = 20(√2 + 1) cm.

4. (Ufu 2017) Um recipiente cônico utilizado em experiências de química deve ter duas marcas horizontais circulares, uma situada a 1 centímetro do vértice do cone, marcando um certo volume v, e outra marcando o dobro deste volume, situada a H centímetros do vértice, conforme figura.

Nestas condições, a distância H, em centímetros, é igual a:

a) ³√2

b) √3

c) 4/3

d) 3/2

Resposta da questão 4:[A]

Do enunciado e da figura, temos:

2V/V = (H/1)³ → 2 = H³ → H = ³√2

5. (Ufu 2017) Um indivíduo com uma grave doença teve a temperatura do corpo medida em intervalos curtos e igualmente espaçados de tempo, levando a equipe médica a deduzir que a temperatura corporal T do paciente, em cada instante t, é bem aproximada pela função T = 36.10^t/100, em que t é medido em horas, e T em graus Celsius. Quando a temperatura corporal deste paciente atingir os 40⁰C, a equipe médica fará uma intervenção, administrando um remédio para baixar a temperatura.

Nestas condições, quantas horas se passarão desde o instante t = 0 até a administração do remédio? Utilize log 9 = 0,95.

a) 5

b) 6

c) 7

d) 8

Resposta da questão 5:[A]

Do enunciado, 40 = 36 . 10^t/100 → 10^t/100 = 40/36 → 10^t/100 = 10/9 →

log 10^t/100 = log 10/9 → t/100 . log10 = log10 – log9 → t/100 . 1 = 1 – 0,95 →

t/100 = 0,05 → t = 100 . 0,05 → t = 5 horas

6. (Ufu 2017) Uma empresa que presta serviços de telefonia rural possui duas torres T₁ e T₂ com específicas áreas de cobertura, correspondendo a círculos C₁ e C₂ que se tangenciam, conforme ilustra a Figura 1.

Essas torres serão desativadas e uma nova torre será instalada de forma que sua área de cobertura corresponda ao círculo C, tangenciando C₁ e C₂, conforme Figura 2.

Se x² + y² – 6x = 0 é a equação cartesiana descrevendo C₁ e a medida da área (sombreada) da ampliação da cobertura é 30πkm², então, o valor do raio, em Km, do círculo C₂ é um número :

a) par

b) múltiplo de 3

c) primo

d) divisível por 7

Resposta da questão 6:[C]

De x² + y² – 6x = 0, temos: x² – 6x + 9 + y² = 0 + 9 → (x - 3)² + (y - 0)² = 3²

O raio de C₁ mede 3 km, com isso, observemos a figura abaixo:

Então, 30π = π.(3 + r)² – π.3² – π.r² → 30π = π.[9 + 6r + r² – 3² – r² ]→

30 = 6r → r = 5.

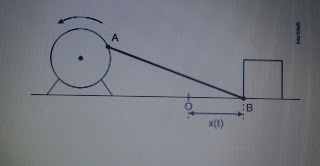
7. (Ufu 2017) Em um determinado sistema mecânico, as extremidades de uma haste rígida AB ficam conectadas, de forma articulada, a um motor e a um corpo, conforme ilustra a figura. Quando o motor é ligado, a haste imprime ao corpo um movimento oscilatório, e a distância horizontal x(t) do ponto B em cada instante t em relação a um ponto fixo O é dado pela expressão x(t) = | (1/2)(sent) + (√3/2)(cost) | centímetros.

Nestas condições, a maior distância x(t), em centímetros, será igual a:

Dados: cos (π/3) = 1/2 e sen (π/3) = √3/2