1. (Unicamp
2018) Sendo
c um número real, considere a função afim f(x) = 2x + c, definida para todo
número real x.
a)
Encontre todas as soluções da equação [f(x)]3 = f(x3),
para c = 1.
b)
Determine todos os valores de c para os quais a função g(x) = log(xf(x) + c)
esteja definida para todo número real x.
a) Para c =
1, temos [f(x)]3 = f(x3)
→ (2x + 1)3 = 2x3 + 1 →
8x3 + 12x2 + 6x + 1 = 2x3 + 1 → 6x3
+ 12x2 + 6x = 0 →
x3 + 2x2 + x
= 0 → x(x2 + 2x + 1) =
0 → x(x + 1)2 = 0 →
x = 0 ou x = - 1.
Portanto, a resposta é x = 0 ou x = - 1
b) Sendo xf(x) + c = x(2x + c) + c = 2x2
+ cx + c, deve-se ter
2x2 + cx + c > 0 para todo x real. Tal condição é satisfeita
se, e somente se, c2 – 4.2.c < 0 → 0 < c < 8.
2. (Unicamp
2018) Considere
a sequência de números reais (a1, a2, a3, a4,
a5) tal que (a1, a2, a3) é uma progressão
geométrica e (a3, a4, a5) é uma progressão
aritmética, ambas com a mesma razão w.
a)
Determine a sequência no caso em que a3 = 3 e w = 2.
b)
Determine todas as sequências tais que a1 = 1 e a5 = 8.
a) Se (a1, a2, a3)
é uma progressão geométrica, a3 = 3 e w = 2, então
(a1, a2, a3) = (3/22 , 3/2,
3) = (3/4, 3/2, 3)
Ademais, se (a3, a4, a5) é uma progressão aritmética, então
(a3, a4, a5) = (3, 3 + 2, 3 + 2.2) = (3, 5, 7).
Portanto, temos (a1, a2, a3, a4,
a5) = (3/4, 3/2, 3, 5, 7)
b) Se a1
= 1 então (a1,
a2, a3, a4, a5) = (1, w, w2,
w2 + w, w2 + 2w).
Mas a5 = 8 e, portanto, vem w2 + 2w = 8 → (w + 1)2
= 9 →
w + 1 = ± 3 → w = - 4 ou w = 2
Em consequência, temos (a1, a2, a3, a4,
a5) = (1, - 4, 16, 12, 8) ou
(a1,
a2, a3, a4, a5) = (1, 2, 4, 6, 8)
3. (Unicamp
2018) Sabendo
que p e q são números reais, considere as matrizes
a)
Prove que para quaisquer p e q teremos BT. AB ≥ 0.
b)
Determine os valores de p e q para os quais o sistema linear nas
variáveis
reais x, y e z, abaixo, tenha infinitas
soluções.
a) Sendo Bt = (p 0
q), temos :
Portanto, como (p + q)2 ≥ 0 para quaisquer p, q ɛ R, segue o
resultado.
b) Tem-se que :
Logo, tomando a matriz ampliada do sistema e
escalonando, vem :
Portanto, se p = 0 e q = 0 ou se p = 1 e q = 1/2 o sistema será possível e indeterminado.
4. (Unicamp 2018)
A figura
abaixo exibe, no plano cartesiano, um quadrilátero com vértices situados nos
pontos de coordenadas A = (-5, 0), B = (5, 0), C = (4, 3) e D = (-3, 4).
a) Determine
a área desse quadrilátero.
b)
Encontre a equação da reta que passa pelo ponto A e é perpendicular à reta que
passa pelos pontos B e C.
a) A área do quadrilátero ABCD é dada por :
b) Desde que o coeficiente angular da
reta que passa por B e C é
(3 - 0)/(4 - 5) = - 3, podemos concluir que a resposta é dada por
y = 0 = - 1/(-3) . (x - ( 5)) → y = x/3 + 5/3
5. (Unicamp 2018)
A figura
abaixo exibe um triângulo com lados de comprimentos a, b e c e ângulos internos
ϴ, 2ϴ e β.
a)
Supondo que o triângulo seja isósceles, determine todos os valores possíveis
para o ângulo ϴ.
b)
Prove que, se c = 2a , então β= 900.
a) O triângulo é isósceles se β = ϴ ou β
= 2ϴ. Logo, no primeiro caso,
temos
4ϴ = 1800 o que implica em ϴ =
450. Já no segundo
caso, temos
5ϴ = 1800 o
que implica em ϴ = 360.
b) Considere a figura, em que P é o pé da
bissetriz do ângulo ABC.
Sendo os ângulos MBP e MAP congruentes,
podemos concluir que o
triângulo ABP é isósceles de base AB. Ademais, se M é o ponto médio
de
AB,
então BM = 2a/2 = a e MP é perpendicular a AB. Daí, como BC = a, BP
é lado comum e MBP ≡ CBP, segue que os
triângulos MBP e CBP são
congruentes por LAL, portanto β = 900
6. (Unicamp 2018)
A tabela
abaixo exibe o valor das mensalidades do Ensino Fundamental em três escolas
particulares nos anos de 2017 e 2018.
|
ANO
|
Escola A
|
Escola B
|
Escola C
|
|
2017
|
R$ 1000,00
|
R$ 1200,00
|
R$ 1500,00
|
|
2018
|
R$ 1150,00
|
R$ 1320,00
|
R$ 1680,00
|
a) Determine
qual escola teve o maior aumento percentual nas mensalidades de 2017 para 2018.
b) Uma
família tem três filhos matriculados na Escola
B. Suponha que essa escola ofereça um desconto de 10% na mensalidade
para o segundo filho e de 20% para o terceiro filho. Calcule o valor a ser
gasto mensalmente com os três filhos em 2018.
a) Desde que os aumentos percentuais
foram
[(1150 - 1000)/1000] . 100% = 15% ;
[(1320 - 1200)/1200] . 100% = 10% e
[(1680 - 1500)/1500] . 100% = 12%
podemos
concluir que a Escola A teve o maior aumento.
b) O resultado é dado por
1320 + 1320.0,9 + 1320.0,8 = R$ 3564,00






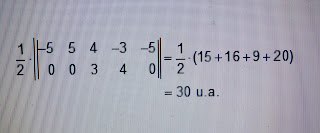


Nenhum comentário:
Postar um comentário